In the kinematic_topology_schema five different kinematic_topology_representations are defined. There must always be a main kinematic_topology_structure that consists of all kinematic_joints and kinematic_links but no other elements. The other four kinematic topology representations define sub-structures, some with higher-level concepts such as tree and loop, within the main kinematic_topology_structure. This is done by re-using the same instances of kinematic_joint and kinematic_link.

For each kinematic_topology_representation there might be zero, one or many mechanism_representations, defined in the kinematic_structure_schema. A mechanism_representation is related to exactly one kinematic_topology_representation and defines a kinematic_pair for each kinematic_joint and a kinematic_link_representation for each kinematic_joint of the referenced kinematic_topology_representation. This is done by the items of a mechanism_representations that are constraint to be of type pair_representation_relationships. A pair_representation_relationships provides the geometric relationship between two kinematic_link_representations for a kinematic_pair. Different mechanism_representations may re-use the same instances of pair_representation_relationship, kinematic_link_representation, and kinematic_pair.

A kinematic_link_representation is related to exactly one kinematic_link. However a kinematic_link may have different kinematic_link_representations that are used in different mechanism_representations. A kinematic_link_representation may be rigid or linear_flexible. A roller chain is an example for a linear_flexible_link_representation. For a kinematic_pair the first link might be either rigid or linear-flexible, however the second link must must always be rigid. A kinematic_link_representation may be related to one or several shape_representation via a kinematic_link_representation_association; e.g. an advanced_brep_shape_representation that represent the geometry of the kinematic_link. Either the kinematic_link_representation and associated shape_representation shall share the same geometric_representation_context, or the kinematic_link_representation_association shall be instantiated together with a representation_relationship_with_transformation.

Each kinematic_pair fall into one of these categories:

• low_order_kinematic_pair;
• low_order_with_motion_constraint_kinematic_pair;
• high_order_kinematic_pair.

In addition each kinematic_pair might be an actuated_kinematic_pair.

A low_order_pair may have up to three translation and three rotation degrees of freedom. Wherever possible on of the specific subtypes shall be used:

• revolute_pair;
• cylindrical_pair;
• spherical_pair;
• spherical_pair_with_pin;
• planar_pair;
• unconstrained_pair;
• fully_constrained_pair;
• prismatic_pair;
• universal_pair.

For most of the specific kinds of kinematic_pair a range subtype is defined to further constrain the degree of freedom within some interval.

The main entity of the kinematic_state_representation_schema is mechanism_state_representation that represents a particular state of a mechanism_representation. The items of a mechanism_state_representation are pair_values, that define a particular state for the kinematic_pairs of the referenced mechanism_representation.

Kinematic motion as defined in the kinematic_motion_representation_schema is controlled along a parameter t whose context is given by a geometric_representation_context_with_parameter. This allows to define a unit for the parameter, e.g. seconds. Kinematic motion can be realised in two different ways:

A interpolated_configuration_representation defines a sequence of mechanism_state_representation at a given parameter value. The transition of one state to another is controlled by interpolation_type. A link_motion_representation_along_path defines a parameter controlled path for each kinematic_link_representation or any kind of shape_representation. This is independent of the availability of a mechanism_representation or kinematic_pair information.

E.2 Hinge example

The example illustrates the kinematics of a simple hinge. The hinge itself (#300) is an assembly of two parts (#100 and #200), each with an associated advanced_shape_representation whose details are not given here. Instances #100 to #312 as well as #900 to #9xx corresponds to current recommended practises and are not further explained here.

Instances #321 amd #322 define a kinematic property and assign the mechansim representation #500 as its representation. The mechanism itself is based on the kinematic_topological_representation #400 that consists of a single joint (#402) with two links (#403 and #404).

For each of the kinematic_link a kinematic_link_representation is defined. Because the links of a hinge are typically rigid the subtype rigid_link_representation (#510,,#520) is used. Each of the kinematic_link_representations contains an axis2_placement_3d that are needed as pair frames for the kinematic_pair. In addition each kinematic_link_representation is associated to the advanced_shape_representation of the of the hinge components via a kinematic_link_representation_association (#513, #523).

The main contents of the hinge mechanism is a kinematic_pair that is a revolute_pair (#503) with a particular range between 0 and 180 degrees. Each kinematic_pair is applying the needed geometric information for a kinematic_joint for which it provides geometric information. In this case these are the references to the axis2_placement_3d (#512 and #522) that define the pair frames. The association with the corresponding kinematic_link_representations is done by the pair_representation_relationship (#502) that is called out as an item for the mechanism_representation.

Instances #610, #620 and #630 define three different states of the same mechanism #500. In this case a revolute_pair_value is used to define the rotations 0, 90 and 180 degree for the revolute pair.

Motion of the hinge is defined by the interpolated_configuration_representation #700. An interpolation sequence with the three segments #703, #704 and #705 is defined for the parameter values 0, 5 and 7 (e.g. seconds). The interpolation type between 0 and 5 and 5 to 7 is synchronous, but the interpolation type for the last segment is discontinuous, indicating that the interpolated_configuration_representation is ending here; it is not cyclic.

Note that the kinematic_link_representations (#510, #520) share the same representation_contexts as the ones used by the advanced_shape_representation (#105, #205). So no additional transformation is needed. Also the mechanism_representation (#500) and the states of this mechanism (#610, #620, #630) share the same representation context. However the representation contexts of the kinematic_topology_structure (#400) and the interpolated_configuration_representation (#700) can not be shared with others.

ISO-10303-21;
HEADER;

FILE_DESCRIPTION(
/* description */ (' '),
/* implementation_level */ '2;1');
FILE_NAME(
/* name */ 'hinge',
/* time_stamp */ '2011-04-15T13:16:22',
/* author */ ('Lothar Klein'),
/* organization */ ('LKSoftWare GmbH'),
/* preprocessor_version */ 'x.x.x - partially hand populated',
/* originating_system */ 'IDA-STEP',
/* authorization */ 'draft');
FILE_SCHEMA(('AP242_MANAGED_MODEL_BASED_3D_ENGINEERING_MIM'));
ENDSEC;
DATA;

/* the first part of the hinge */
#100=PRODUCT('4711-1','Hinge Part A',$,(#902));
#101=PRODUCT_DEFINITION_FORMATION('',$,#100);
#102=PRODUCT_DEFINITION('1',$,#101,#903);
#103=PRODUCT_DEFINITION_SHAPE('',$,#102);
#104=SHAPE_DEFINITION_REPRESENTATION(#103,#105);
#105=ADVANCED_BREP_SHAPE_REPRESENTATION('',(#107,...),#106);
#106=(GEOMETRIC_REPRESENTATION_CONTEXT(3)
      GLOBAL_UNIT_ASSIGNED_CONTEXT((...))
      REPRESENTATION_CONTEXT('',''));
#107=AXIS2_PLACEMENT_3D(...);      

/* the second part of the hinge */
#200=PRODUCT('4711-2','Hinge Part B',$,(#902));
#201=PRODUCT_DEFINITION_FORMATION('',$,#200);
#202=PRODUCT_DEFINITION('1',$,#201,#06);
#203=PRODUCT_DEFINITION_SHAPE('',$,#202);
#204=SHAPE_DEFINITION_REPRESENTATION(#203,#205);
#205=ADVANCED_BREP_SHAPE_REPRESENTATION('',(#207,...),#206);
#206=(GEOMETRIC_REPRESENTATION_CONTEXT(3)
      GLOBAL_UNIT_ASSIGNED_CONTEXT((...))
      REPRESENTATION_CONTEXT('',''));
#207=AXIS2_PLACEMENT_3D(...);      

/* the hinge itself, an assembly of the first and second part with a kinematic property */
#300=PRODUCT('4711','Hinge',$,(#902));
#301=PRODUCT_DEFINITION_FORMATION('',$,#300);
#302=PRODUCT_DEFINITION('1',$,#301,#903);
#303=PRODUCT_DEFINITION_CONTEXT_ASSOCIATION(#302,#904,#905);
#311=NEXT_ASSEMBLY_USAGE_OCCURRENCE('1','',$,#302,#102,'1');
#312=NEXT_ASSEMBLY_USAGE_OCCURRENCE('2','',$,#302,#202,'2');

#320=PRODUCT_DEFINITION_KINEMATICS('',$,#302);
#321=KINEMATIC_PROPERTY_MECHANISM_REPRESENTATION(#320,#500,#510);
#330=PRODUCT_DEFINITION_RELATIONSHIP_KINEMATICS('',$,#311);
#331=CONTEXT_DEPENDENT_KINEMATIC_LINK_REPRESENTATION(#513,#330);
#340=PRODUCT_DEFINITION_RELATIONSHIP_KINEMATICS('',$,#312);
#341=CONTEXT_DEPENDENT_KINEMATIC_LINK_REPRESENTATION(#523,#340);

/* Kinematic topology */
#400=KINEMATIC_TOPOLOGY_STRUCTURE('',(#402),#401);
#401=REPRESENTATION_CONTEXT('','');
#402=KINEMATIC_JOINT('',#403,#404);
#403=KINEMATIC_LINK('L1');
#404=KINEMATIC_LINK('L2');

/* Mechanism */
#500=MECHANISM_REPRESENTATION('',(#502),#501,#400);
#501=(GEOMETRIC_REPRESENTATION_CONTEXT(3)
      GLOBAL_UNIT_ASSIGNED_CONTEXT((...))
      REPRESENTATION_CONTEXT('',''));
#502=PAIR_REPRESENTATION_RELATIONSHIP('','',$,#510,#520,#503);   
#503=REVOLUTE_PAIR_WITH_RANGE('',*,'pair-X',#512,#522,#402,*,*,*,*,*,*,0,180); 

#510=RIGID_LINK_REPRESENTATION('',(#512),#106,#403);
#512=AXIS2_PLACEMENT_3D(...);      
#513=KINEMATIC_LINK_REPRESENTATION_ASSOCIATION('',$,#510,#105);

#520=RIGID_LINK_REPRESENTATION('',(#522),#206,#404);
#522=AXIS2_PLACEMENT_3D(...);      
#523=KINEMATIC_LINK_REPRESENTATION_ASSOCIATION('',$,#520,#205);

/* Kinematic state 1, 2 and 3 */
#610=MECHANISM_STATE_REPRESENTATION('state-1',(#612),*,#500);
#612=REVOLUTE_PAIR_VALUE('',#503,0);      

#620=MECHANISM_STATE_REPRESENTATION('state-2',(#622),*,#500);
#622=REVOLUTE_PAIR_VALUE('',#503,90);      

#630=MECHANISM_STATE_REPRESENTATION('state-3',(#632),*,#500);
#632=REVOLUTE_PAIR_VALUE('',#503,180);      

/* kinematic motion */
#700=INTERPOLATED_CONFIGURATION_REPRESENTATION('',(#702),#701);
#701=(GEOMETRIC_REPRESENTATION_CONTEXT(3)
      GEOMETRIC_REPRESENTATION_CONTEXT_WITH_PARAMETER($)
      GLOBAL_UNIT_ASSIGNED_CONTEXT((...))
      REPRESENTATION_CONTEXT('',''));
#702=INTERPOLATED_CONFIGURATION_SEQUENCE('',(#703,#704,#705));
#703=INTERPOLATED_CONFIGURATION_SEGMENT(#610,0,.SYNCHRONOUS_INTERPOLATION_TYPE.);
#704=INTERPOLATED_CONFIGURATION_SEGMENT(#620,5,.SYNCHRONOUS_INTERPOLATION_TYPE.);
#705=INTERPOLATED_CONFIGURATION_SEGMENT(#630,7,.DISCONTINUOUS_INTERPOLATION_TYPE.);

/* auxiliary stuff */
#900=APPLICATION_PROTOCOL_DEFINITION('CD','AP242_MANAGED_MODEL_BASED_3D_ENGINEERING_MIM','2011',#901);
#901=APPLICATION_CONTEXT('mechanical design');
#902=PRODUCT_CONTEXT('part',#901,'');
#903=PRODUCT_DEFINITION_CONTEXT('part definition',#901,'design');
#904=PRODUCT_DEFINITION_CONTEXT('assembly definition',#901,'design');
#905=PRODUCT_DEFINITION_CONTEXT_ROLE('part definition type',$);
#906=PRODUCT_RELATED_PRODUCT_CATEGORY('part',$,(#100,#200,#300));
#910=APPLIED_ORGANIZATION_ASSIGNMENT(#912,#911,(#100,#200,#300));
#911=ORGANIZATION_ROLE('id owner');
#912=ORGANIZATION('No.1','John Doe Ltd.','company');

/* missing
   - details of ABREPS
   - units
   - action/action_method to which the motion is associated
*/   

ENDSEC;
END-ISO-10303-21;

	

A ypr_rotation. defines a sequence of three rotations about the yaw, pitch, and roll axes (in this order). In this part of ISO 10303, this rotation sequence is applied mainly to frames; in the case of a spherical_pair_value, e.g., it relates the axis directions of the pair frame on the second link of a spherical_pair to the axis directions of the pair frame on the first link of the same pair. It may be applied, however, to any vector-valued quantity in R ³.

Let

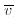
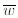
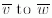
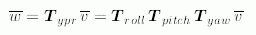
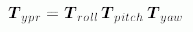
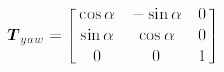
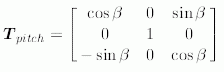
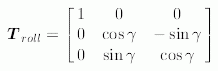
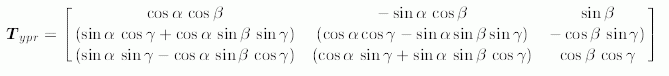
The function compute_rotation_matrix_from_ypr_rotation computes the rotation matrix which corresponds to a ypr_rotation, given by its angles yaw, pitch, and roll, according to the notation specified in E.1. The function returns an ARRAY [1 : 3] OF ARRAY [1 : 3] OF REAL.

NOTE 1   This function is provided as an example for applications which need rotations to be given in matrix notation rather than in terms of ypr angles. It should fit into a schema that USEs or REFERENCEs the kinematic_structure_schema.

NOTE 2   The term 'rotation matrix' is not used uniquely within the scientific community. The result of compute_rotation_matrix_from_ypr_rotation is valid only for a notation as used in E.1.

FUNCTION compute_rotation_matrix_from_ypr_rotation
		 (yaw		: REAL;
		  pitch		: REAL;
		  roll		: REAL;
		  factor	: REAL)
				: ARRAY [1 : 3] OF ARRAY [1 : 3] OF REAL;
  LOCAL
	y, p, r	: REAL;
	result	: ARRAY [1 : 3] OF ARRAY [1 : 3] OF REAL;
  END_LOCAL;

  y := factor * yaw;
  p := factor * pitch;
  r := factor * roll;
  
  result := [ [	COS(y) * COS(p),
	-	SIN(y) * COS(p),
		SIN(p) ],
	[	SIN(y) * COS(r) + COS(y) * SIN(p) * SIN(r),
		COS(y) * COS(r) - SIN(y) * SIN(p) * SIN(r),
	-	COS(p) * SIN(r) ],
	[	SIN(y) * SIN(r) - COS(y) * SIN(p) * COS(r),
		COS(y) * SIN(r) + SIN(y) * SIN(p) * COS(r),
		COS(p) * COS(r) ] ];
  RETURN (result);
END_FUNCTION;
	 

Argument definitions:

yaw: the yaw angle of the ypr_rotation which is being evaluated.

NOTE 3   For an attribute ypr of type ypr_rotation in an entity e, the actual parameter for yaw could be either e.ypr[ypr index(ypr enumeration.yaw)] or just e.ypr[3].

pitch: The pitch angle of the ypr_rotation which is being evaluated.

NOTE 4   For an attribute ypr of type ypr_rotation in an entity e, the actual parameter for pitch could be either e.ypr[ypr index(ypr enumeration.pitch)] or just e.ypr[1].

roll: The roll angle of the ypr_rotation which is being evaluated.

NOTE 5   For an attribute ypr of type ypr_rotation in an entity e, the actual parameter for roll could be either e.ypr[ypr index(ypr enumeration.roll)] or just e.ypr[2].

factor: The conversion factor that is required to convert yaw, pitch, and roll into equivalent angle measurements using radian as the plane angle unit.

NOTE 6   ISO 10303-11 requires the parameters of the SIN and COS functions to be expressed in radians.

The principle of the DH-notation is to relate a target frame on a link (denoted k, e.g.) to that pair frame on the preceeding link (denoted k - 1) in the kinematic chain which belongs to the pair by which link k is connected to link k - 1. The target frame may either be a pair frame of another pair on link k or any other frame on link k, e.g., a tool center point frame. The four DH-parameters a_k ^DH , α_k ^DH , θ_k ^DH , and s_k ^DH define the transformation from the relating pair frame on link k - 1 to the target frame on link k, including the motion in the pair shared by both links. See [2] for details of the DH-notation.

The use of DH-parameters is commonly restricted to links that are connected to their predecessor by either a revolute pair or a prismatic pair. One could imagine its application also to cylindrical pairs and to screw pairs.

When using SU-parameters, the relationship between the pair frames of the shared pair is separated from the kinematic link description. The pair is characterised by a transformation involving the pair parameters, which is specific to the pair type, whereas the link data relevant to kinematics are constant transformations from an arbitrarily chosen, but fixed link frame to the various pair frames on the same link. See su_parameters.

A pair and a link whose data are specified using DH-notation can easily be redefined using SU-notation. The resulting frame definition will probably not take full advantage of the exibility given by the SU-notation, but it will be a valid definition. The following paragraphs provide a guidance to such a redefinition. The 'target frame' of the DH-notation is chosen as the link frame of link k, as it is usually done implicitly also with the DH-notation. The SU-parameters for the pair frame on link k which mates with the 'relating' pair frame on the preceeding link k - 1 are derived from the inverse of the transformation matrix defined by the DH-parameters, with zero pair parameters. Angles are given in radians; occasionally, the given values have to be replaced by the equivalent values in the plane angle units that are actually used by an application.

Revolute pair: For a link k connected to its predecessor k - 1 by a revolute pair, the pair transformation corresponds essentially to the yaw rotation as given in E.1, replacing there α by the pair parameter θ_k ^DH . The SU-parameters for the pair frame of the revolute pair on link k, as defined in su_parameters, are found by setting a_k = a_k ^DH , α_k = α_k ^DH , b_k = -s_k ^DH , β_k = π, c_k = 0, and γ_k = π.

Prismatic pair: For a link k connected to its predecessor k - 1 by a prismatic pair, the pair transformation is a pure translational transformation along the z-axes, with s_k ^DH being the pair parameter. The SU-parameters for the pair frame of the prismatic pair on link k are found by setting a_k = a_k ^DH , α_k = α_k ^DH , b_k = 0, β_k = π - θ_k ^DH , c_k = 0, and γ_k = π.

Cylindrical pair and screw pair: For a link k connected to its predecessor k - 1 by a cylindrical pair or by a screw pair, the pair transformation is composed of a translational transformation along the z-axes (pair parameter s_k ^DH ) and a rotational yaw transformation (pair parameter θ_k ^DH ). In the case of a cylindrical pair, the pair parameters s_k ^DH and θ_k ^DH are independent one from the other, whereas for a screw pair one of them depends functionally on the other (see screw_pair_value). The SU-parameters for the pair frame of the cylindrical pair or of the screw pair on link k are found by setting a_k = a_k ^DH , α_k = α_k ^DH , b_k = 0, β_k = π, c_k = 0, and γ_k = π. Here it is supposed that both pair frames of the cylindrical or screw pair coincide if both parameters, s_k ^DH and θ_k ^DH , are equal to zero.

© ISO 2019 — All rights reserved