Overview

When working with geometry, it is often useful to talk about the volume of space containing a shape. The most commonly used volume is an axis-aligned bounding box, which can be easily calculated from a set of points, combined, or intersected. Testing whether a point lies within one is quick.

All definitions are in the rose_bounds.h header file.

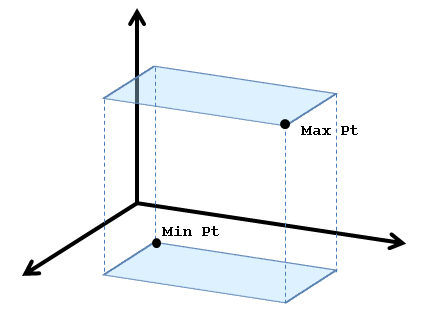
The RoseBoundingBox class describes an axis-aligned bounding box. This box is formed by a pair of XY planes at the maximum and minimum Z coordinates, XZ planes at the max/min Y coordinates, and YZ planes at the max/min X coordinates. The class holds a pair of points that contain the maximum and minimum coordinate values, as shown below:

The RoseBoundingBox2D class describes a rectangle in the XY plane or UV space. The rectangle is formed by vertical and horizontal lines at the upper and lower coordinates. The class holds a pair of points that contain the maximum and minimum 2D coordinate values.

You can compute the boolean union of two bounding boxes with the update() member function and compute the boolean intersection of two volumes with the rose_bounds_intersect() function.

rose_bounds_intersect()

int rose_bounds_intersect(
	RoseBoundingBox& result,
	const RoseBoundingBox& box1,
	const RoseBoundingBox& box2,
	double tol=0
	);

int rose_bounds2d_intersect(
	RoseBoundingBox2D& result,
	const RoseBoundingBox2D& box1,
	const RoseBoundingBox2D& box2,
	double tol=0
	);

The rose_bounds_intersect() function calculates the overlapping volume between two bounding boxes and returns true if the result is not empty. The bounds of the intersection region is stored in the result parameter. The rose_bounds2d_intersect() function is a 2D version that works with bounding rectangles.

By default, strict numeric comparison is used to determine whether there is any overlap. If the boxes overlap exactly at a face, say box1.minx() exactly equals box2.maxx(), the function will return true but the result will have zero thickness in the X direction.

If the optional tol value is given, the function uses a box that extends tol further on each side when checking for overlap with the other bounding box. The value can be negative if you need to shrink the box.

When the faces are within tol of each other, but not overlapping, the result volume will contain the distance between the faces, which may be zero if the faces overlap exactly. If the boxes overlap corner to corner, the closest points could be up to tol*ROSE_SQRT_3 apart in 3D or tol*ROSE_SQRT_2 apart in 2D.

// define box -1,-1,-1 to 10,10,10
RoseBoundingBox b1;
b1.update(-1, -1, -1);
b1.update(10,10,10);

// define box 9,9,9 to 12,12,12
RoseBoundingBox b2;
b2.update(9, 9, 9);
b2.update(12, 12, 12);

// define box 10.1,10.1,10.1 to 12,12,12
RoseBoundingBox b3;
b3.update(10.1, 10.1, 10.1);
b3.update(12, 12, 12);

RoseBoundingBox res;

// good overlap ==> true
// result box 9, 9, 9 to 10, 10, 10
rose_bounds_intersect(res, b1, b2);

// slightly separated ==> false
// result box empty
rose_bounds_intersect(res, b1, b3);

// slightly separated, but add 0.5 all around ==> true
// result box 10, 10, 10 to 10.1, 10.1, 10.1
rose_bounds_intersect(res, b1, b3, 0.5);