The part 21 file example below illustrates how this AIC may be used to show the logical relationships between the domains of topological constructs. This is a section of a part 21 file showing all the relevant geometry and topology definitions.

EXAMPLE 1 /* Geometry Definition of original closed shell -
 shell is in shape of a cube with half cylinder on top. */
#1040 =(LENGTH_UNIT()NAMED_UNIT(*)SI_UNIT(.MILLI.,.METRE.));
#1041 =(NAMED_UNIT(*)PLANE_ANGLE_UNIT()SI_UNIT($,.RADIAN.));
#1100 = CARTESIAN_POINT(’origin’,(0.0,0.0,0.0));
#1101 = DIRECTION(’Dir1’,(1.0,0.0,0.0));
#1102 = DIRECTION(’Dir2’,(0.0,1.0,0.0));
#1103 = DIRECTION(’Dir3’,(0.0,0.0,1.0));
#1104 = DIRECTION(’NegX’,(-1.0,0.0,0.0));
/* Points and vertices for face boundaries of closed shell. */
#1105 = VERTEX_POINT(’VertPtO’,#1100);
#1106 = CARTESIAN_POINT(’PtA’,(100.0, 0.0, 0.0));
#1107 = VERTEX_POINT(’VertPtA’,#1106);
#1108 = CARTESIAN_POINT(’PtB’,(100.0, 100.0, 0.0));
#1109 = VERTEX_POINT(’VertPtB’,#1108);
#1110 = CARTESIAN_POINT(’PtC’,(0.0, 100.0, 0.0));
#1111 = VERTEX_POINT(’VertPtC’,#1110);
#1112 = CARTESIAN_POINT(’PtD’,(0.0, 0.0 ,100.0));
#1113 = VERTEX_POINT(’VertPtD’,#1112);
#1114 = CARTESIAN_POINT(’PtE’,(100.0, 0.0 ,100.0));
#1115 = VERTEX_POINT(’VertPtE’,#1114);
#1116 = CARTESIAN_POINT(’PtF’,(100.0, 100.0, 100.0));
#1117 = VERTEX_POINT(’VertPtF’,#1116);
#1118 = CARTESIAN_POINT(’PtG’,(0.0, 100.0, 100.0));
#1119 = VERTEX_POINT(’VertPtG’,#1118);
/* Surfaces for faces */
#1120 = AXIS2_PLACEMENT_3D(’Ax2P3DBase’,#1100,#1103,#1101);
#1121 = PLANE(’Baseplane’, #1120);
#1122 = AXIS2_PLACEMENT_3D(’Ax2P3DFront’,#1100,#1101,#1102);
#1123 = PLANE(’Frontplane’, #1122);
#1124 = AXIS2_PLACEMENT_3D(’Ax2P3DRight’,#1100,#1102,#1103);
#1125 = PLANE(’Rightplane’, #1124);
#1126 = AXIS2_PLACEMENT_3D(’Ax2P3DLeft’,#1110,#1102,#1103);
#1127 = PLANE(’Leftplane’, #1126);
#1128 = AXIS2_PLACEMENT_3D(’Ax2P3DBack’,#1106,#1101,#1102);
#1129 = PLANE(’Backplane’, #1128);
#1130 = CARTESIAN_POINT(’CentreCyl’,(50.0, 0.0, 100.0));
#1131 = AXIS2_PLACEMENT_3D(’Ax2P3DCyl’,#1130,#1102,#1104);
#1132 = CYLINDRICAL_SURFACE(’TopCyl’,#1131, 50.0);
/* Curves and edge_curves */
#1140 = AXIS2_PLACEMENT_3D(’Ax2P3DLcirc’,#1154,#1102,#1104);
#1141 = VECTOR(’VecX’,#1101, 100.0);
#1142 = VECTOR(’VecY’,#1102, 100.0);
#1143 = VECTOR(’VecZ’,#1103, 100.0);
#1144 = LINE(’LineOA’,#1100, #1141);
#1145 = LINE(’LineOC’,#1100, #1142);
#1146 = LINE(’LineOD’,#1100, #1143);
#1147 = LINE(’LineAE’,#1106, #1143);
#1148 = LINE(’LineAB’,#1106, #1142);
#1149 = LINE(’LineCG’,#1110, #1143);
#1150 = LINE(’LineCB’,#1110, #1141);
#1151 = LINE(’LineDG’,#1112, #1142);
#1152 = LINE(’LineEF’,#1114, #1142);
#1153 = CIRCLE(’RtCirc’,#1131, 50.0);
#1154 = CARTESIAN_POINT(’CentreLcirc’,(50.0, 100.0, 100.0));
#1155 = LINE(’LineBF’,#1108,#1143);
#1156 = CIRCLE(’LCirc’,#1140, 50.0);
#1157 = EDGE_CURVE(’EdgeOA’,#1105,#1107,#1144,.T.);
#1158 = EDGE_CURVE(’EdgeOC’,#1105,#1111,#1145,.T.);
#1159 = EDGE_CURVE(’EdgeOD’,#1105,#1113,#1146,.T.);
#1160 = EDGE_CURVE(’EdgeAE’,#1107,#1115,#1147,.T.);
#1161 = EDGE_CURVE(’EdgeAB’,#1107,#1109,#1148,.T.);
#1162 = EDGE_CURVE(’EdgeCG’,#1111,#1119,#1149,.T.);
#1163 = EDGE_CURVE(’EdgeCB’,#1111,#1109,#1150,.T.);
#1164 = EDGE_CURVE(’EdgeDG’,#1113,#1119,#1151,.T.);
#1165 = EDGE_CURVE(’EdgeEF’,#1115,#1117,#1152,.T.);
#1166 = EDGE_CURVE(’EdgeDE’,#1113,#1115,#1153,.T.);
#1167 = EDGE_CURVE(’EdgeGF’,#1119,#1117,#1156,.T.);
#1168 = EDGE_CURVE(’EdgeBF’,#1109,#1117,#1155,.T.);
/* oriented_edges */
#1169 = ORIENTED_EDGE(’OAT’,*,*,#1157,.T.);
#1170 = ORIENTED_EDGE(’OAF’,*,*,#1157,.F.);
#1171 = ORIENTED_EDGE(’OCT’,*,*,#1158,.T.);
#1172 = ORIENTED_EDGE(’OCF’,*,*,#1158,.F.);
#1173 = ORIENTED_EDGE(’ODT’,*,*,#1159,.T.);
#1174 = ORIENTED_EDGE(’ODF’,*,*,#1159,.F.);
#1175 = ORIENTED_EDGE(’AET’,*,*,#1160,.T.);
#1176 = ORIENTED_EDGE(’AEF’,*,*,#1160,.F.);
#1177 = ORIENTED_EDGE(’ABT’,*,*,#1161,.T.);
#1178 = ORIENTED_EDGE(’ABF’,*,*,#1161,.F.);
#1179 = ORIENTED_EDGE(’CGT’,*,*,#1162,.T.);
#1180 = ORIENTED_EDGE(’CGF’,*,*,#1162,.F.);
#1181 = ORIENTED_EDGE(’CBT’,*,*,#1163,.T.);
#1182 = ORIENTED_EDGE(’CBF’,*,*,#1163,.F.);
#1183 = ORIENTED_EDGE(’DGT’,*,*,#1164,.T.);
#1184 = ORIENTED_EDGE(’DGF’,*,*,#1164,.F.);
#1185 = ORIENTED_EDGE(’EFT’,*,*,#1165,.T.);
#1186 = ORIENTED_EDGE(’EFF’,*,*,#1165,.F.);
#1187 = ORIENTED_EDGE(’DET’,*,*,#1166,.T.);
#1188 = ORIENTED_EDGE(’DEF’,*,*,#1166,.F.);
#1189 = ORIENTED_EDGE(’GFT’,*,*,#1167,.T.);
#1190 = ORIENTED_EDGE(’GFF’,*,*,#1167,.F.);
#1191 = ORIENTED_EDGE(’BFT’,*,*,#1168,.T.);
#1192 = ORIENTED_EDGE(’BFF’,*,*,#1168,.F.);
/* edge_loops */
#1201 = EDGE_LOOP(’ELOCBA’,(#1171, #1181, #1178, #1170));
#1202 = EDGE_LOOP(’ELOAED’,(#1169, #1175, #1188, #1174));
#1203 = EDGE_LOOP(’ELODGC’,(#1173, #1183, #1180, #1172));
#1204 = EDGE_LOOP(’ELABFE’,(#1177, #1191, #1186, #1176));
#1205 = EDGE_LOOP(’ELCGFB’,(#1179, #1189, #1192, #1182));
#1206 = EDGE_LOOP(’ELDEFG’,(#1187, #1185, #1190, #1184));
/* face_bounds and advanced_faces */
#1211 = FACE_OUTER_BOUND(’baseBd’,#1201,.T.);
#1212 = FACE_OUTER_BOUND(’rightBd’,#1202,.T.);
#1213 = FACE_OUTER_BOUND(’frontBd’,#1203,.T.);
#1214 = FACE_OUTER_BOUND(’backBd’,#1204,.T.);
#1215 = FACE_OUTER_BOUND(’leftBd’,#1205,.T.);
#1216 = FACE_OUTER_BOUND(’TopcylBd’,#1206,.T.);
#1221 = ADVANCED_FACE(’BaseFace’,(#1211),#1121,.F.);
#1222 = ADVANCED_FACE(’RightFace’,(#1212),#1125,.F.);
#1223 = ADVANCED_FACE(’FrontFace’,(#1213),#1123,.F.);
#1224 = ADVANCED_FACE(’BackFace’,(#1214),#1129,.T.);
#1225 = ADVANCED_FACE(’LeftFace’,(#1215),#1127,.T.);
#1226 = ADVANCED_FACE(’TopcylFaceO’,(#1216),#1132,.T.);
/* closed_shell */
#1250 = CLOSED_SHELL(’CubeCyl’, (#1221, #1222, #1223, #1224, #1225, #1226));
/* New point and vertex for subset1, M is 1/3 of way along semi-circle GF */
#1300 = CARTESIAN_POINT(’PtM’,(25.0, 100.0, 143.3012702));
#1301 = VERTEX_POINT(’VertPtM’, #1300);
/* Edge DM is defined as a surface curve on cylindrical face via a pcurve.
 Define 2D context and 2D geometry for pcurve (line in parameter space) */
#1302 = (GEOMETRIC_REPRESENTATION_CONTEXT(2)
	 PARAMETRIC_REPRESENTATION_CONTEXT()
	 REPRESENTATION_CONTEXT(’CylSurf’,’Parameter_space’));
#1303 = CARTESIAN_POINT(’PtOparam’,(0.0, 0.0));
#1304 = DIRECTION(’Dir2D’, (1.047197551, 100.0));
#1305 = VECTOR(’Vec2D’, #1304, 100.013708);
#1306 = LINE(’LinPcrv’, #1303, #1305);
#1307 = DEFINITIONAL_REPRESENTATION(’Pcurvrep’, (#1306), #1302);
#1308 = PCURVE(’CylPcrv’, #1132, #1307);
/* Define approximate 3D geometry of surface curve D to M */
#1310 = CARTESIAN_POINT(’P2’, (0.0, 33.33333333, 117.4532952));
#1311 = CARTESIAN_POINT(’P3’, (9.885005297, 66.666666667, 134.5746238));
#1312 = BEZIER_CURVE(’CylCrv3D’, 3, (#1112, #1310, #1311, #1300),
	   .UNSPECIFIED., .F., .F.);
#1313 = SURFACE_CURVE(’CrvBM3D’, #1312, (#1308), .PCURVE_S1.);
/* Define new edges for subset 1. */
#1321 = EDGE_CURVE(’EdgeDM’, #1113, #1301, #1313, .T. );
#1322 = ORIENTED_EDGE(’DMT’, *, *, #1321, .T.);
#1323 = SUBEDGE(’EdgeGM’, #1119, #1301, #1167);
#1324 = ORIENTED_EDGE(’GMF’, *, *, #1323, .F.);
/* Define subface and subset 1 (as cfss and open_shell). */
#1325 = EDGE_LOOP(’ELDMG’, (#1322, #1324, #1184));
#1326 = FACE_OUTER_BOUND(’SubCylFac1Bd’, #1325, .T.);
#1327 = SUBFACE(’SubCylF1’, (#1326), #1236);
#1350 = (CONNECTED_FACE_SET( (#1327, #1223))
	CONNECTED_FACE_SUB_SET(#1250)
	OPEN_SHELL( )
	REPRESENTATION_ITEM(’Subset1’)
	TOPOLOGICAL_REPRESENTATION_ITEM( ));
/* Define new edges and associated geometry for subset 2 (inside Subset1). */
#1400 = CARTESIAN_POINT(’PtP’,(0.0, 65.0, 50.0));
#1401 = VERTEX_POINT(’VertPtP’, #1400);
#1402 = CARTESIAN_POINT(’PtQ’,(0.0, 65.0, 100.0));
#1403 = VERTEX_POINT(’VertPtQ’, #1402);
#1404 = CARTESIAN_POINT(’PtR’,(10.0, 65.0, 130.0));
#1405 = VERTEX_POINT(’VertPtR’, #1404);
#1406 = CARTESIAN_POINT(’PtS’,(10.0, 90.0, 130.0));
#1407 = VERTEX_POINT(’VertPtS’, #1406);
#1408 = CARTESIAN_POINT(’PtT’,(0.0, 90.0, 100.0));
#1409 = VERTEX_POINT(’VertPtT’, #1408);
#1410 = CARTESIAN_POINT(’PtU’,(0.0, 90.0, 50.0));
#1411 = VERTEX_POINT(’VertPtU’, #1410);
#1412 = LINE(’LinePQ’, #1400, #1143);
#1413 = LINE(’LinePU’, #1400, #1142);
#1414 = LINE(’LineRS’, #1404, #1142);
#1415 = LINE(’LineUT’, #1410, #1143);
#1416 = CARTESIAN_POINT(’CentreCirc2’,(50.0, 65.0, 100.0));
#1417 = AXIS2_PLACEMENT_3D(’Ax2P3DCirc2’,#1416,#1102,#1104);
#1418 = CIRCLE(’Circ2’,#1417, 50.0);
#1419 = CARTESIAN_POINT(’CentreCirc3’,(50.0, 90.0, 100.0));
#1420 = AXIS2_PLACEMENT_3D(’Ax2P3DCirc3’,#1419,#1102,#1104);
#1421 = CIRCLE(’Circ3’,#1420, 50.0);
#1422 = EDGE_CURVE(’EdgePQ’, #1401, #1403, #1412, .T.);
#1423 = EDGE_CURVE(’EdgePU’, #1401, #1411, #1413, .T.);
#1424 = EDGE_CURVE(’EdgeRS’, #1405, #1407, #1414, .T.);
#1425 = EDGE_CURVE(’EdgeUT’, #1411, #1409, #1415, .T.);
#1426 = EDGE_CURVE(’EdgeQR’, #1403, #1405, #1418, .T.);
#1427 = EDGE_CURVE(’EdgeTS’, #1409, #1407, #1421, .T.);
#1428 = SUBEDGE(’EdgeQT’, #1403, #1409, #1164);
/* Define edge_loops, face_bounds and subfaces */
#1429 = ORIENTED_EDGE(’PQT’, *, *, #1422, .T.);
#1430 = ORIENTED_EDGE(’PUF’, *, *, #1423, .F.);
#1431 = ORIENTED_EDGE(’RST’, *, *, #1424, .T.);
#1432 = ORIENTED_EDGE(’UTF’, *, *, #1425, .F.);
#1433 = ORIENTED_EDGE(’QRT’, *, *, #1426, .T.);
#1434 = ORIENTED_EDGE(’TSF’, *, *, #1427, .F.);
#1435 = ORIENTED_EDGE(’QTT’, *, *, #1428, .T.);
#1436 = ORIENTED_EDGE(’QTF’, *, *, #1428, .F.);
#1437 = EDGE_LOOP(’ELPQTU’, (#1429, #1435, #1432, #1430));
#1438 = EDGE_LOOP(’ELQRST’, (#1433, #1431, #1434, #1436));
#1439 = FACE_OUTER_BOUND(’SubCylFac2Bd’, #1438, .T.);
#1440 = FACE_OUTER_BOUND(’SubFrontBd’, #1437, .T.);
#1441 = SUBFACE(’SubCylF2’, (#1439), #1327);
#1442 = SUBFACE(’SubFront’, (#1440), #1223);
#1450 = (CONNECTED_FACE_SET( (#1441, #1442))
	CONNECTED_FACE_SUB_SET(#1350)
	OPEN_SHELL( )
	REPRESENTATION_ITEM(’Subset2’)
	TOPOLOGICAL_REPRESENTATION_ITEM( ));
#1490 = (GEOMETRIC_REPRESENTATION_CONTEXT(3)
	GLOBAL_UNIT_ASSIGNED_CONTEXT((#1040,#1041))
	REPRESENTATION_CONTEXT(’Context for Subsets’,
	’This is a 3D context using millimetres’));
#1500 = MANIFOLD_SUBSURFACE_SHAPE_REPRESENTATION(’SubsetRep’,
	(#1350, #1450), #1490);

NOTE 1   #1250 is a closed_shell in the form of a cube with a half cylinder on top. It has 6 faces, 5 of them planar, with a cylindrical top face. This could be used to define an advanced_brep_shape_representation from ISO 10303-514 [3], or a manifold_surface_shape_representation from ISO 10303-509 [2]. For the purpose of naming the faces and describing the geometry it is assumed that the closed shell is being viewed from a point along the negative X axis with the Z axis pointing towards the top of the cylindrical face.

NOTE 2   #1350 defines an instance of open_shell and connected_face_sub_set that refers to #1250 as its parent_face_set. It consists of 2 faces, one of these is the front face from #1250 and the second is a subface of the cylindrical top face of #1250. One of the edges of this triangular subface is a subedge, one is an existing edge and the third has its geometry defined by a pcurve on the cylindrical surface. This pcurve is a line in parameter space from the point (0,0) to (π/3, 100). A Bezier curve provides a slightly less precise 3 dimensional representation of this surface_curve.

NOTE 3   #1450 illustrates the possibility of nesting connected face_sub_sets. It is defined with #1350 as parent_face_set. It consists of two subfaces, each related to a face of #1350. The shared edge between these subfaces is another example of a subedge.

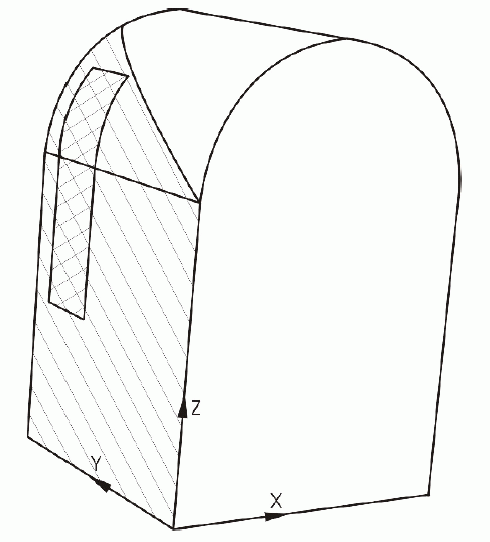
NOTE 4   #1500 is an instance of manifold_subsurface_shape_representation containing connected face sub_sets #1350 and #1450. It is defined in a 3 dimensional geometric_representation_context using millimetres and radians as units. This provides the context for all 3D geometry in the file. The geometry defined in this file is illustrated in figure E.1.

© ISO 2011 — All rights reserved