
| Integrated generic resource: Geometric and topological representation | ISO 10303-42:2021(E) © ISO |
The subject of the geometry_schema is the geometry of parametric curves and surfaces. The representation_schema (see ISO 10303-43) and the geometric_representation_context defined in this Part of ISO 10303, provide the context in which the geometry is defined. The geometric_representation_context enables a distinction to be made between those items which are in the same context, and thus geometrically related, and those existing in independent coordinate spaces. In particular, each geometric_representation_item has a geometric_representation_context which includes as an attribute the Euclidean dimension of its coordinate space. The coordinate system for this space is referred to as the geometric coordinate system in this clause. Units associated with length_measures and plane_angle_measures are assumed to be assigned globally within this context. A global rule (compatible_dimension) ensures that all geometric_representation_items in the same geometric_representation_context have the same space dimensionality. The space dimensionality dim is a derived attribute of all subtypes of geometric_representation_item.
This clause defines the information requirements to which implementations shall conform using the EXPRESS language as defined in ISO 10303-11. The following EXPRESS declaration begins the geometry_schema and identifies the necessary external references.Each implementation of an AP that uses this schema and that encodes entity names shall use the encoding specified in Annex A. Each reference to this schema in an open system shall use the identifier encoding specified in Annex B. This schema is illustrated in Annex D using the EXPRESS-G notation.
EXPRESS specification:
*)
SCHEMA geometry_schema;
REFERENCE FROM
geometric_model_schema
--
ISO 10303-42
(block,
boolean_result,
cyclide_segment_solid,
eccentric_cone,
edge_based_wireframe_model,
ellipsoid,
face_based_surface_model,
faceted_primitive,
geometric_set,
half_space_solid,
primitive_2d,
rectangular_pyramid,
right_angular_wedge,
right_circular_cone,
right_circular_cylinder,
shell_based_surface_model,
shell_based_wireframe_model,
solid_model,
sphere,
tessellated_item,
torus);
REFERENCE FROM
measure_schema
--
ISO 10303-41
(global_unit_assigned_context,
length_measure,
parameter_value,
plane_angle_measure,
plane_angle_unit,
positive_length_measure,
positive_plane_angle_measure);
REFERENCE FROM
representation_schema
--
ISO 10303-43
(definitional_representation,
founded_item,
functionally_defined_transformation,
item_in_context,
representation,
representation_context,
representation_item,
using_representations);
REFERENCE FROM
scan_data_3d_shape_model_schema
--
ISO 10303-42
(scanned_data_item);
REFERENCE FROM
topology_schema
--
ISO 10303-42
(edge_curve,
face_surface,
poly_loop,
vertex_point,
volume_with_faces);
(*
NOTE 1 The schemas referenced above are specified in the following parts:
geometric_model_schema ISO 10303-42 measure_schema ISO 10303-41 representation_schema ISO 10303-43 scan_data_3d_shape_model_schema ISO 10303-42 topology_schema ISO 10303-42
NOTE 2 See Annex D for a graphical representation of this schema.
4.2.1 Space Dimensionality
All geometry shall be defined in a right-handed rectangular Cartesian coordinate system with the same units on each axis. A common scheme has been used for the definition of both two-dimensional and three-dimensional geometry. Points and directions exist in both a two-dimensional and a three-dimensional form; these forms are distinguished solely by the presence, or absence, of a third coordinate value. Complex geometric entities are all defined using points and directions from which their space dimensionality can be deduced.
4.2.2 Geometric relationships
All geometric_representation_items which are included as items in a representation having a geometric_representation_context are geometrically related. Any such geometric_representation_item is said to be geometrically founded in the context of that representation. No geometric relationship, such as distance between points, is assumed to exist for geometric_representation_items occurring as items in different representations.
4.2.3 Parametrisation of analytic curves and surfaces
Each curve or surface specified here has a defined parametrisation. In some instances the definitions are in parametric terms. In others, the conic curves and elementary surfaces, the definitions are in geometric terms. In this latter case a placement coordinate system is used to define the parametrisation. The geometric definitions contain some, but not all, of the data required for this. The relevant data to define this placement coordinate system is contained in the axis2_placement associated with the individual curve and surface entities. Where the curve or surface parameterisation uses trigonometric functions, the parameter for the function behaves like an angle and can be considered to be an angular parameter. Numerical values for such angular parameters shall use the current units for plane_angle_measure.
4.2.4 Curves
The curve entities defined in this schema include lines, elementary conics, a general parametric polynominal curve, and some referentially or procedurally defined curves. All the curves have a well defined parametrisation which makes it possible to trim a curve or identify points on the curve by parameter value. The geometric direction of a curve is the direction of increasing parameter value. For the conic curves, a method of representation is used which separates their geometric form from their orientation and position in space. In each case, the position and orientation information is conveyed by an axis2_placement. The general purpose parametric curve is represented by the b_spline_curve entity. This was selected as the most stable form of representation for the communication of all types of polynomial and rational parametric curves. With appropriate attribute values and subtypes, a b_spline_curve entity is capable of representing single span or spline curves of explicit polynomial, rational, Bézier or B-spline type. A composite_curve entity, which includes the facility to communicate continuity information at the curve-to-curve transition points, is provided for the construction of more complex curves.
The offset_curve and curve_on_surface types are curves defined with reference to other geometry. Separate offset_curve entities exist for 2D and 3D applications. The curve on surface entities include an intersection_curve which represents the intersection of two surfaces. Such a curve may be represented in 3D space or in the 2D parameter space of either of the surfaces.
4.2.5 Surfaces
The surface entities support the requirements of simple boundary representation (B-rep) solid modelling system and enable the communication of general polynomial and rational parametric surfaces. The simple surfaces are the planar, spherical, cylindrical, conical and toroidal surfaces, a surface_of_revolution and a surface_of_linear_extrusion. As with curves, all surfaces have an associated standard parametrisation. In many cases the surfaces, as defined, are unbounded; it is assumed that they will be bounded either explicitly or implicitly. Explicit bounding is achieved with the rectangular_trimmed_surface or curve_bounded_surface entities; implicit bounding requires the association of additional topological information to define a face.
The b_spline_surface entity and its subtypes provide the most general capability for the communication of all types of polynomial and rational biparametric surfaces. This entity uses control points as the most stable form of representation for the surface geometry. The offset_surface entity is intended for the communication of a surface obtained as a simple normal offset from a given surface. The rectangular_composite_surface entity provides the basic capability to connect together a rectangular mesh of distinct surface patches, specifying the degree of continuity from patch to patch.
4.2.6 Preferred form
Some of the geometric entities provide the potential capability of defining an item of geometry in more than one way. Such multiple representations are accommodated by requiring the nomination of a `preferred form' or `master representation'. This is the form which is used to determine the parametrisation.
NOTE The master_representation attribute acknowledges the impracticality of ensuring that multiple forms are indeed identical and allows the indication of a preferred form. This would probably be determined by the creator of the data. All characteristics, such as parametrisation, domain, and results of evaluation, for an entity having multiple representations, are derived from the master representation. Any use of the other representations is a compromise for practical considerations.
Table 1 — Geometry mathematical symbology
|
Symbol |
Definition |
|---|---|
| a | Scalar quantity |
| A | Vector quantity |
| < > | Vector normalisation |
| a | Normalised vector < A > = A / | A | |
| × | Vector (cross) product |
| ⋅ | Scalar product |
| A → B | A is transformed to B |
| λ (u) | Parametric curve |
| σ (u,v) | Parametric surface |
| S(x,y,z) | Analytic surface |
| C x | Partial differential of C with respect to x |
| σ u | Partial differential of σ (u,v) with respect to u |
| S x | Partial derivative of S with respect to x |
| | | | Absolute value, or magnitude or determinant |
| R m | m-dimensional real space |
EXPRESS specification:
*)
CONSTANT
(*
A dummy_gri is a partial entity definition to be used when types of geometric_representation_item are constructed. It provides the correct supertypes and the name attribute as an empty string.
EXPRESS specification:
*)
dummy_gri
: geometric_representation_item := representation_item('')|| geometric_representation_item();
(*
*)
END_CONSTANT;
(*

NOTE This select type enables entities requiring axis placement information to reference the axes without specifying the space dimensionality.
EXPRESS specification:
*)
TYPE
axis2_placement
=
SELECT
(axis2_placement_2d,
axis2_placement_3d);
END_TYPE;
(*

EXPRESS specification:
*)
TYPE
b_spline_curve_form
=
ENUMERATION
OF
(polyline_form,
circular_arc,
elliptic_arc,
parabolic_arc,
hyperbolic_arc,
unspecified);
END_TYPE;
(*
Enumerated item definitions:
polyline_form: a connected sequence of line segments represented by degree 1 B-spline basis functions;
circular_arc: an arc of a circle, or a complete circle represented by a B-spline curve;
elliptic_arc: an arc of ellipse, or a complete ellipse represented by a B-spline curve;
parabolic_arc: an arc of finite length of a parabola represented by a B-spline curve;
hyperbolic_arc: an arc of finite length of an hyperbola represented by a B-spline curve;
unspecified: a curve for which no particular form is specified;

EXPRESS specification:
*)
TYPE
b_spline_surface_form
=
ENUMERATION
OF
(plane_surf,
cylindrical_surf,
conical_surf,
spherical_surf,
toroidal_surf,
surf_of_revolution,
ruled_surf,
generalised_cone,
quadric_surf,
surf_of_linear_extrusion,
unspecified);
END_TYPE;
(*
Enumerated item definitions:
plane_surf: a bounded portion of a plane represented by a B-spline surface of degree 1 in each parameter;
cylindrical_surf: a bounded portion of a cylindrical surface;
conical_surf: a bounded portion of a right circular cone;
spherical_surf: a bounded portion of a sphere, or a complete sphere, represented by a B-spline surface;
toroidal_surf: a torus, or portion of a torus, represented by a B-spline surface;
surf_of_revolution: a bounded portion of a surface of revolution;
ruled_surf: a surface constructed from two parametric curves by joining with straight lines corresponding points with the same parameter value on each of the curves.
generalised_cone: a special case of a ruled surface in which the second curve degenerates to a single point; when represented by a B-spline surface all the control points along one edge will be coincident;
quadric_surf: a bounded portion of one of the class of surfaces of degree 2 in the variables x, y and z;
surf_of_linear_extrusion: a bounded portion of a surface of linear extrusion represented by a B-spline surface of degree 1 in one of the parameters;
unspecified: a surface for which no particular form is specified;

The curve_on_surface is a curve on a parametric surface. It may be a pcurve, or a surface_curve including the specialised subtypes of intersection_curve and seam_curve, or a composite_curve_on_surface.
EXPRESS specification:
*)
TYPE
curve_on_surface
=
SELECT
(composite_curve_on_surface,
pcurve,
surface_curve);
END_TYPE;
(*

EXPRESS specification:
*)
TYPE
dimension_count
=
INTEGER;
WHERE
WR1: SELF > 0;
END_TYPE;
(*
Formal propositions:
WR1: A dimension_count shall be positive.

EXPRESS specification:
*)
TYPE
extent_enumeration
=
ENUMERATION
OF
(invalid,
zero,
finite_non_zero,
infinite);
END_TYPE;
(*
Enumerated item definitions:
invalid: the concept of extent is not valid for the quantity being measured;
zero: the extent is zero;
finite_non_zero: the extent is finite (bounded) but not zero;
infinite: the extent is not finite;

EXPRESS specification:
*)
TYPE
knot_type
=
ENUMERATION
OF
(uniform_knots,
quasi_uniform_knots,
piecewise_bezier_knots,
unspecified);
END_TYPE;
(*
Enumerated item definitions:
uniform_knots: the form of knots appropriate for a uniform B-spline curve or surface;
quasi_uniform_knots: the form of knots appropriate for a quasi-uniform B-spline curve or surface;
piecewise_bezier_knots: the form of knots appropriate for a piecewise Bézier curve;
unspecified: the type of knots is not specified; this includes the case of non uniform knots;

EXPRESS specification:
*)
TYPE
linearly_independent_enum
=
ENUMERATION
OF
(independent,
not_independent,
not_tested);
END_TYPE;
(*
Enumerated item definitions:
independent: the set of combined B-spline functions is linearly independent;
not_independent: the set of B-spline functions is linearly dependent;
not_tested: the set of B-spline functions has not been tested for linear dependence.

NOTE See [6], [7] and [15] for further details of the specific types of locally refined splines.
EXPRESS specification:
*)
TYPE
locally_refined_spline_type_enum
=
ENUMERATION
OF
(analysis_suitable_t_spline,
hierarchical_b_spline,
lr_b_spline,
semi_standard_t_spline,
standard_t_spline);
END_TYPE;
(*
Enumerated item definitions:
analysis_suitable_t_spline: the local B-spline is of the analysis suitable t-spline type;
hierarchical_b_spline: the local B-spline is of the hierachical b-spline type;
lr_b_spline: the local B-spline is of the lr-b-spline type;
semi_standard_t_spline: the local B-spline is of the semi-standard t-spline type;
standard_t_spline: the local B-spline is of the standard t-spline type;

EXPRESS specification:
*)
TYPE
pcurve_or_surface
=
SELECT
(pcurve,
surface);
END_TYPE;
(*

EXPRESS specification:
*)
TYPE
preferred_surface_curve_representation
=
ENUMERATION
OF
(curve_3d,
pcurve_s1,
pcurve_s2);
END_TYPE;
(*
Enumerated item definitions:
curve_3d: the curve in three-dimensional space is preferred;
pcurve_s1: the first pcurve is preferred;
pcurve_s2: the second pcurve is preferred;

EXPRESS specification:
*)
TYPE
spline_knot_values
=
LIST[2:?] OF REAL;
WHERE
WR1: increasing_values_in_list(SELF);
END_TYPE;
(*
Formal propositions:
WR1: The knot values shall be strictly increasing in size.

EXPRESS specification:
*)
TYPE
surface_boundary
=
SELECT
(boundary_curve,
degenerate_pcurve);
END_TYPE;
(*

EXPRESS specification:
*)
TYPE
transition_code
=
ENUMERATION
OF
(discontinuous,
continuous,
cont_same_gradient,
cont_same_gradient_same_curvature);
END_TYPE;
(*
Enumerated item definitions:
discontinuous: the segments, or patches, do not join; this is permitted only at the boundary of the curve or surface to indicate that it is not closed.
continuous: the segments, or patches, join, but no condition on their tangents is implied;
cont_same_gradient: the segments, or patches, join, and their tangent vectors, or tangent planes, are parallel and have the same direction at the joint; equality of derivatives is not required;
cont_same_gradient_same_curvature: the gradient and curvature are continuous; for a curve, the segments join, their tangent vectors are parallel and in the same direction, and their curvatures are equal at the joint; equality of derivatives is not required; for a surface this implies that the principal curvatures are the same and that the principal directions are coincident along the common boundary.

EXPRESS specification:
*)
TYPE
trimming_preference
=
ENUMERATION
OF
(cartesian,
parameter,
unspecified);
END_TYPE;
(*
Enumerated item definitions:
cartesian: trimming by cartesian point is preferred;
parameter: trimming by parameter value is preferred;;
unspecified: no trimming preference is communicated;

EXPRESS specification:
*)
TYPE
trimming_select
=
SELECT
(cartesian_point,
parameter_value);
END_TYPE;
(*

EXPRESS specification:
*)
TYPE
vector_or_direction
=
SELECT
(direction,
vector);
END_TYPE;
(*

A geometric_representation_context is a type of representation_context in which geometric_representation_item s are geometrically founded.
A geometric_representation_context is a distinct coordinate space, spatially unrelated to other coordinate spaces except as those coordinate spaces are specifically related by an appropriate transformation. (See 3.2 for definitions of geometrically founded and coordinate space.)
EXPRESS specification:
*)
ENTITY geometric_representation_context
SUBTYPE OF (representation_context);
coordinate_space_dimension : dimension_count;
END_ENTITY;
(*
Attribute definitions:
coordinate_space_dimension: the number of dimensions of the coordinate space which is the geometric_representation_context
NOTE Any constraints on the allowed range of coordinate_space_dimension are outside the scope of this part of ISO 10303.

A geometric_representation_item is a type of representation_item that has the additional meaning of having geometric position or orientation or both.
This meaning is present by virtue of:
NOTE 1 An indirect reference to a cartesian_point or a direction means that a given geometric_representation_item references the cartesian_point or direction through one or more intervening attributes. In many cases this information is given in the form of an axis2_placement .
EXAMPLE 1 Consider a circle. It gains its geometric position and orientation by virtue of a reference to an axis2_placement that in turn references a cartesian_point and several direction s.
EXAMPLE 2 A manifold_solid_brep is a geometric_representation_item that through several layers of topological_representation_item s, references curve s, surface s and point s. Through additional intervening entities curves and surfaces reference cartesian_point and direction .
NOTE 2 The intervening entities, which are all of type representation_item , need not be of subtype geometric_representation_item . Consider the manifold_solid_brep from the above example. One of the intervening levels of representation_item is a closed_shell . This is a topological_representation_item and does not require a geometric_representation_context in its own right. When used as part of the definition of a manifold_solid_brep that itself is a geometric_representation_item , it is founded in a geometric_representation_context .
NOTE 3 A geometric_representation_item inherits the need to be related to a representation_context in a representation.
NOTE 4 As subtypes of representation_item there is an implicit and/or relationship between geometric_representation_item and topological_representation_item . The only complex instances intended to be created are edge_curve , face_surface , and vertex_point
EXPRESS specification:
*)
ENTITY geometric_representation_item
SUPERTYPE OF (ONEOF (point,
direction,
vector,
placement,
cartesian_transformation_operator,
curve,
surface,
edge_curve,
face_surface,
poly_loop,
vertex_point,
solid_model,
boolean_result,
sphere,
right_circular_cone,
right_circular_cylinder,
torus,
block,
primitive_2d,
right_angular_wedge,
ellipsoid,
faceted_primitive,
rectangular_pyramid,
cyclide_segment_solid,
volume,
half_space_solid,
shell_based_surface_model,
face_based_surface_model,
shell_based_wireframe_model,
edge_based_wireframe_model,
geometric_set,
tessellated_item,
volume_with_faces,
scanned_data_item))
SUBTYPE OF (representation_item);
DERIVE
dim : dimension_count := dimension_of(SELF);
WHERE
WR1: SIZEOF (QUERY (using_rep <* using_representations (SELF) | NOT ('GEOMETRY_SCHEMA.GEOMETRIC_REPRESENTATION_CONTEXT' IN
TYPEOF (using_rep.context_of_items)))) = 0;
END_ENTITY;
(*
Attribute definitions:
dim: the coordinate dimension_count of the geometric_representation_item .
Formal propositions:
WR1: The context of any representation referencing a geometric_representation_item" shall be a geometric_representation_context .
NOTE 5 The dim attribute is derived from the coordinate_space_dimension of a geometric_representation_context in which the geometric_representation_item is geometrically founded.
NOTE 6 A geometric_representation_item is geometrically founded in one or more geometric_representation_context s, all of which have the same coordinate_space_dimension . See the rule compatible_dimension .

A point is a type of geometric_representation_item and is a location in some real Cartesian coordinate space R m , for m = 1 2 or 3.
EXPRESS specification:
*)
ENTITY point
SUPERTYPE OF (ONEOF (cartesian_point,
point_on_curve,
point_on_surface,
point_in_volume,
point_replica,
degenerate_pcurve))
SUBTYPE OF (geometric_representation_item);
END_ENTITY;
(*

NOTE 1 For the purposes of defining geometry in this part of ISO 10303 only two or three-dimensional points are used.
NOTE 2 Depending upon the geometric_representation_context in which the point is used the names of the coordinates may be (x,y,z) , or (u,v), or any other chosen values.
EXPRESS specification:
*)
ENTITY cartesian_point
SUPERTYPE OF (ONEOF (cylindrical_point,
polar_point,
spherical_point))
SUBTYPE OF (point);
coordinates : LIST[1:3] OF length_measure;
END_ENTITY;
(*
Attribute definitions:
coordinates: the ordered list of 1, 2 or 3 coordinate values, according to the dimensionality of the space in which the point is defined;
coordinates[1] The component in the direction of the first axis, X or, in parameter space u;
coordinates[2] The component in the direction of the second axis Y, or in a parameter space v;
coordinates[3] The component in the direction of the Z axis; this will not be present in the case of a cartesian_point in a two-dimensional coordinate space.

EXPRESS specification:
*)
ENTITY cylindrical_point
SUBTYPE OF (cartesian_point);
r : length_measure;
theta : plane_angle_measure;
z : length_measure;
DERIVE
SELF\cartesian_point.coordinates : LIST[3:3] OF length_measure := [r*cos(theta), r*sin(theta), z];
WHERE
WR1: r >= 0.0;
END_ENTITY;
(*
Attribute definitions:
r: the distance from the point to the z axis;
theta: the angle between the plane containing the point and the z axis and the xz plane;
z: the distance from the xy plane to the point.
coordinates: the rectangular cartesian coordinates of this point;
Formal propositions:
WR1: The radius r shall be greater than, or equal to zero.
Informal propositions:
IP1: The value of theta shall lie in the range 0 ≤ theta 0 < 360°.

EXPRESS specification:
*)
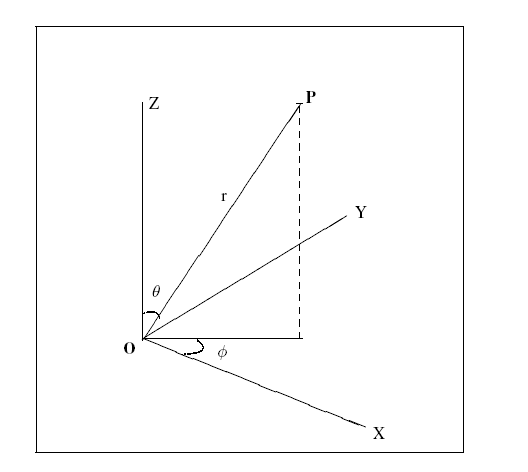
ENTITY spherical_point
SUBTYPE OF (cartesian_point);
r : length_measure;
theta : plane_angle_measure;
phi : plane_angle_measure;
DERIVE
SELF\cartesian_point.coordinates : LIST[3:3] OF length_measure := [r*sin(theta)*cos(phi), r*sin(theta)*sin(phi), r*cos(theta)];
WHERE
WR1: r >= 0.0;
END_ENTITY;
(*
Attribute definitions:
r: the distance from the point to the z axis;
theta: the angle θ between the z axis and the line joining the origin to the point;
phi: the angle φ measured from the x axis to the projection onto the xy plane of the line from the origin to the point.
coordinates: the rectangular cartesian coordinates of this point;
NOTE See Figure (2) for an illustration of the attributes.
Formal propositions:
WR1: The radius r shall be greater than, or equal to zero.
Informal propositions:
IP1: The value of theta shall lie in the range 0 ≤ theta ≤ 180°.
IP2: The value of phi shall lie in the range 0 ≤ phi 0 < 360°.

EXPRESS specification:
*)
ENTITY polar_point
SUBTYPE OF (cartesian_point);
r : length_measure;
theta : plane_angle_measure;
DERIVE
SELF\cartesian_point.coordinates : LIST[2:2] OF length_measure := [r*cos(theta), r*sin(theta)];
WHERE
WR1: r >= 0.0;
END_ENTITY;
(*
Attribute definitions:
r: the distance from the point to the origin;
theta: the angle between the x axis and the line joining the origin to the point.
coordinates: the rectangular cartesian coordinates of this point;
Formal propositions:
WR1: The radius r shall be greater than, or equal to zero.
Informal propositions:
IP1: The value of theta shall lie in the range 0 ≤ theta < 360°.

EXPRESS specification:
*)
ENTITY point_on_curve
SUBTYPE OF (point);
basis_curve : curve;
point_parameter : parameter_value;
END_ENTITY;
(*
Attribute definitions:
basis_curve: the curve to which point_parameter relates;
point_parameter: the parameter value of the point location;
Informal propositions:
IP1: The value of the point_parameter shall not be outside the parametric range of the basis_curve .

EXPRESS specification:
*)
ENTITY point_on_surface
SUBTYPE OF (point);
basis_surface : surface;
point_parameter_u : parameter_value;
point_parameter_v : parameter_value;
END_ENTITY;
(*
Attribute definitions:
basis_surface: the surface to which parameter values relate;
point_parameter_u: the first parameter value of the point location;
point_parameter_v: the second parameter value of the point location.
Informal propositions:
IP1: The parametric values specified for u and v shall not be outside the parametric range of the basis_surface .

EXPRESS specification:
*)
ENTITY point_in_volume
SUBTYPE OF (point);
basis_volume : volume;
point_parameter_u : parameter_value;
point_parameter_v : parameter_value;
point_parameter_w : parameter_value;
END_ENTITY;
(*
Attribute definitions:
basis_volume: the volume to which parameter values relate;
point_parameter_u: the first parameter value of the point location;
point_parameter_v: the second parameter value of the point location.
point_parameter_w: the third parameter value of the point location.
Informal propositions:
IP1: The parametric values specified for u, v and w shall not be outside the parametric range of the basis_volume .

EXPRESS specification:
*)
ENTITY point_replica
SUBTYPE OF (point);
parent_pt : point;
transformation : cartesian_transformation_operator;
WHERE
WR1: transformation.dim = parent_pt.dim;
WR2: acyclic_point_replica (SELF,parent_pt);
END_ENTITY;
(*
Attribute definitions:
parent_pt: the point to be replicated;
transformation: the Cartesian transformation operator which defines the location of the point replica.
Formal propositions:
WR1: The coordinate space dimensionality of the transformation attribute shall be the same as that of the parent_pt .
WR2: A point_replica shall not participate in its own definition.

NOTE For example, the apex of a cone could be represented as a degenerate_pcurve .
EXPRESS specification:
*)
ENTITY degenerate_pcurve
SUBTYPE OF (point);
basis_surface : surface;
reference_to_curve : definitional_representation;
WHERE
WR1: SIZEOF(reference_to_curve\representation.items) = 1;
WR2: 'GEOMETRY_SCHEMA.CURVE' IN TYPEOF (reference_to_curve\representation.items[1]);
WR3: reference_to_curve\representation. items[1]\geometric_representation_item.dim =2;
END_ENTITY;
(*
Attribute definitions:
basis_surface: the surface on which the degenerate_pcurve lies;
reference_to_curve: the association of the degenerate_pcurve and the parameter space curve which degenerates to the (equivalent) point.
Formal propositions:
WR1: The set of items in the definitional_representation entity corresponding to the reference_to_curve shall have exactly one element
WR2: The unique item in the set shall be a curve .
WR3: The dimensionality of this parameter space curve shall be 2.
Informal propositions:
IP1: Regarded as a curve in model space, the degenerate_pcurve shall have zero arc length.

NOTE For example, the apex of a cone could be represented as a evaluated_degenerate_pcurve .
EXPRESS specification:
*)
ENTITY evaluated_degenerate_pcurve
SUBTYPE OF (degenerate_pcurve);
equivalent_point : cartesian_point;
END_ENTITY;
(*
Attribute definitions:
equivalent_point: the explicit point in the geometric coordinate system represented by the degenerate pcurve.

NOTE 1 The components of this entity are not normalised. If a unit vector is required it should be normalised before use.
EXPRESS specification:
*)
ENTITY direction
SUBTYPE OF (geometric_representation_item);
direction_ratios : LIST[2:3] OF REAL;
WHERE
WR1: SIZEOF(QUERY(tmp <* direction_ratios | tmp <> 0.0)) > 0;
END_ENTITY;
(*
Attribute definitions:
direction_ratios: list of REAL;
NOTE 2 The direction_ratios attribute is a list, the individual elements of this list are defined below.
direction_ratios[1] The component in the direction of the first axis, X or, in parameter space u;
direction_ratios[2] The component in the direction of the second axis Y, or in a parameter space v;
direction_ratios[3] The component in the direction of the Z axis; this will not be present in the case of a direction in a two-dimensional coordinate space.
Formal propositions:
WR1: The magnitude of the direction vector shall be greater than zero.

NOTE The magnitude of the vector must not be calculated from the components of the orientation attribute. This form of representation was selected to reduce problems with numerical instability. For example a vector of magnitude 2.0 mm and equally inclined to the coordinate axes could be represented with orientation attribute of (1.0,1.0,1.0) and magnitude attribute 2.0.
EXPRESS specification:
*)
ENTITY vector
SUBTYPE OF (geometric_representation_item);
orientation : direction;
magnitude : length_measure;
WHERE
WR1: magnitude >= 0.0;
END_ENTITY;
(*
Attribute definitions:
orientation: the direction of the vector .
magnitude: the magnntude of the vector . All vector s of magnitude 0.0 are regarded as equal in value regardless of the orientation attribute.
Formal propositions:
WR1: The magnitude shall be positive or zero.

EXPRESS specification:
*)
ENTITY placement
SUPERTYPE OF (ONEOF (axis1_placement,
axis2_placement_2d,
axis2_placement_3d))
SUBTYPE OF (geometric_representation_item);
location : cartesian_point;
END_ENTITY;
(*
Attribute definitions:
location: the geometric position of a reference point, such as the centre of a circle, of the item to be located

EXPRESS specification:
*)
ENTITY axis1_placement
SUBTYPE OF (placement);
axis :
OPTIONAL
direction;
DERIVE
z : direction := NVL(normalise(axis), dummy_gri || direction([0.0,0.0,1.0]));
WHERE
WR1: SELF\geometric_representation_item.dim = 3;
END_ENTITY;
(*
Attribute definitions:
axis: the direction of the local Z axis;
z: the normalised direction of the local Z axis;
Formal propositions:
WR1: The coordinate space dimensionality shall be 3.

EXPRESS specification:
*)
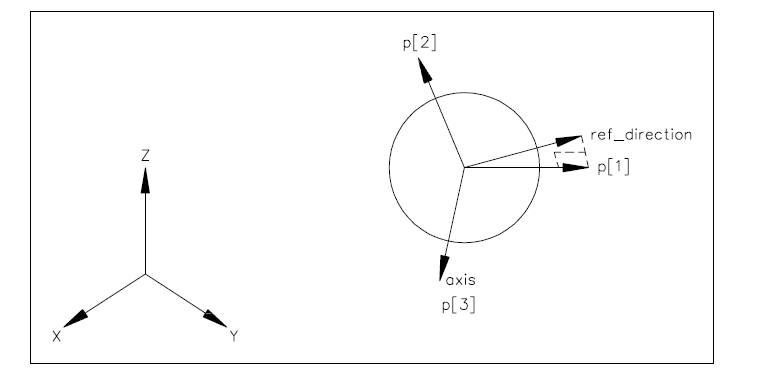
ENTITY axis2_placement_2d
SUBTYPE OF (placement);
ref_direction :
OPTIONAL
direction;
DERIVE
p : LIST[2:2] OF direction := build_2axes(ref_direction);
WHERE
WR1: SELF\geometric_representation_item.dim = 2;
END_ENTITY;
(*
Attribute definitions:
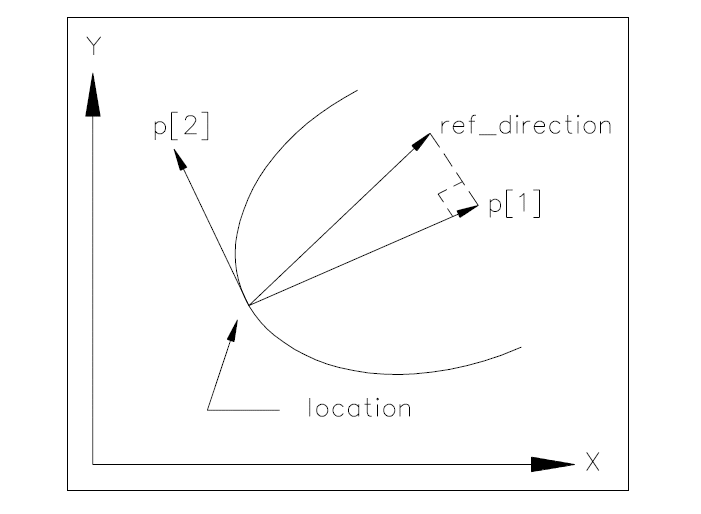
ref_direction: the direction used to determine the direction of the local X axis. If ref_direction is omitted, this direction is taken from the geometric coordinate system;
p: the axis set for the placement coordinate system.
p[1] The normalised direction of the placement X axis. This is (1.0,0.0) if ref_direction is omitted.
p[2] The normalised direction of the placement Y axis. This is a derived attribute and is orthogonal to p[1] .
Formal propositions:
WR1: The space dimensionality of the axis2_placement_2d shall be 2.

NOTE Let z be the placement Z axis direction and a be the approximate placement X axis direction. There are two methods, mathematically identical but numerically different, for calculating the placement X and Y axis directions.
a) The vector a is projected onto the plane defined by the origin point P and the vector z to give the placement X axis direction as
x = < a - (a ⋅ z)z >. The placement Y axis direction is then given by y = < z × x >.
b) The placement Y axis direction is calculated as y = < z × a > and then the placement X axis direction is given by x = < y \× z > .
The first method is likely to be the more numerically stable of the two, and is used here.
A placement coordinate system referenced by the parametric equations is derived from the axis2_placement_3d data for conic curves and elementary surfaces.EXPRESS specification:
*)
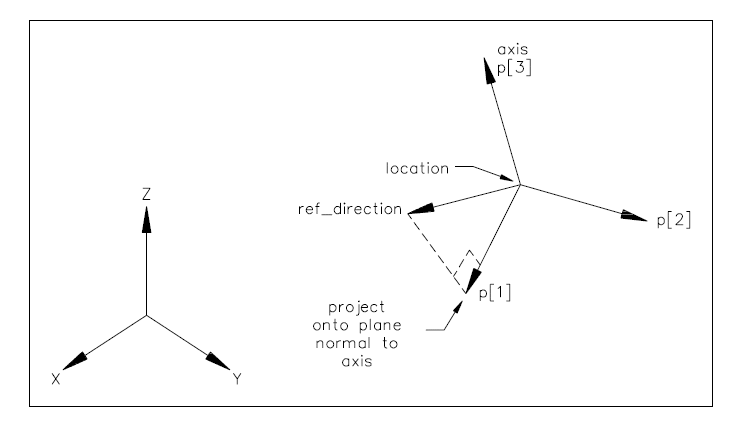
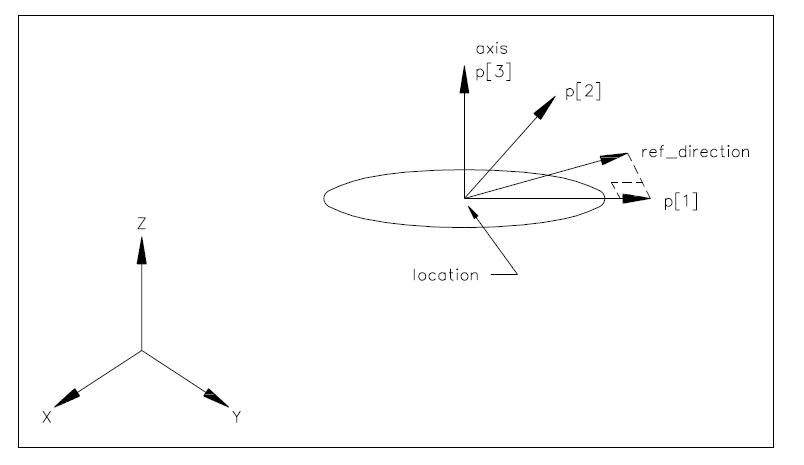
ENTITY axis2_placement_3d
SUBTYPE OF (placement);
axis :
OPTIONAL
direction;
ref_direction :
OPTIONAL
direction;
DERIVE
p : LIST[3:3] OF direction := build_axes(axis,ref_direction);
WHERE
WR1: SELF\placement.location.dim = 3;
WR2: (NOT (EXISTS (axis))) OR (axis.dim = 3);
WR3: (NOT (EXISTS (ref_direction))) OR (ref_direction.dim = 3);
WR4: (NOT (EXISTS (axis))) OR (NOT (EXISTS (ref_direction))) OR (cross_product(axis,ref_direction).magnitude > 0.0);
END_ENTITY;
(*
Attribute definitions:
axis: the exact direction of the local Z axis;
ref_direction: the direction used to determine the direction of the local X axis; if necessary an adjustment is made to maintain orthogonality to the axis direction. If axis and/or ref_direction is omitted, these directions are taken from the geometric coordinate system;
p: the axes for the placement coordinate system. The directions of these axes are derived from the attributes, with appropriate default values if required.
p[1] The normalised direction of the local X axis.
p[2] The normalised direction of the local Y axis.
p[3] The normalised direction of the local Z axis.
NOTE See Figure (3) for interpretation of attributes.
Formal propositions:
WR1: The space dimensionality of the location shall be 3.
WR2: The space dimensionality of axis shall be 3.
WR3: The space dimensionality of ref_direction shall be 3.
WR4: The axis and the ref_direction shall not be parallel or anti-parallel. (This is required by the build_axes function.)

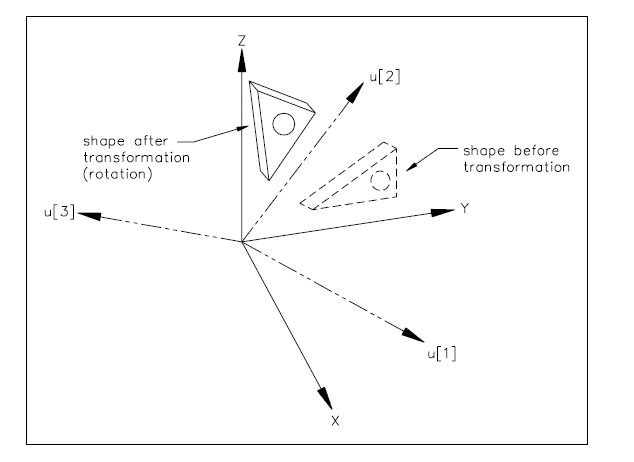
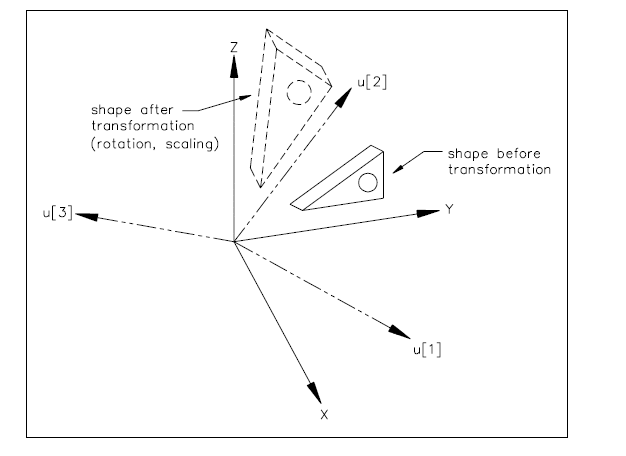
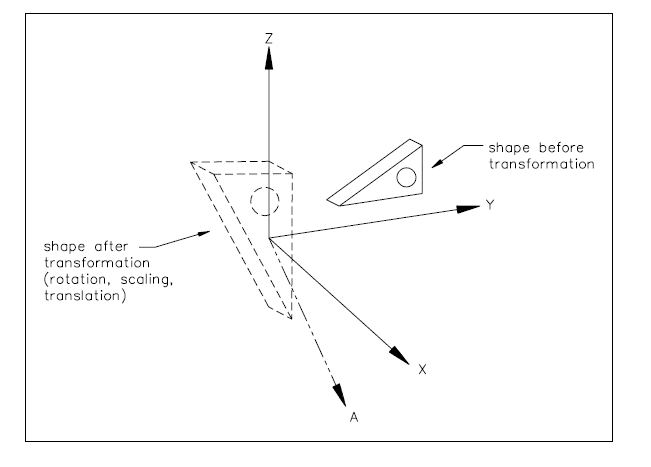
A cartesian_transformation_operator is a type of geometric_representation_item and functionally_defined_transformation , that defines a geometric transformation composed of translation, rotation, mirroring and uniform scaling. The list of normalised vectors u defines the columns of an orthogonal matrix T . These vectors are computed, by the base_axis function, from the direction attributes axis1, axis2 and, in cartesian_transformation_operator_3d, axis3 .
If | T |= -1, the transformation includes mirroring.
The local origin point A , the scale value S and the matrix T together define a transformation.
The transformation for a point with position vector P is defined by
P → A + S TP
The transformation for a direction d is defined by
d → Td
The transformation for a vector with orientation d and magnitude k is defined by
d → Td and k → Sk
For those entities whose attributes include an axis2_placement, the transformation is applied, after the derivation, to the derived attributes p defining the placement coordinate directions. For a transformed surface, the direction of the surface normal at any point is obtained by transforming the normal, at the corresponding point, to the original surface. The parametrisation of the transformed surface is defined using the transformed value of p as defined above. For geometric entities with attributes (such as the radius of a circle) which have the dimensionality of length, the values will be multiplied by S.
For transformations involving reflection or mirroring, with |T|= -1, the relationship between the sense of the boundary and the interior of a curve_bounded_surface, or face_surface is affected.
For a curve_bounded_surface if n is the direction of the surface normal and t is the direction of the tangent vector at a point on the boundary after transformation, then the interior is in the direction |T| n × t
For a face or face_surface, if |T|= -1 the interior of the transformed face will lie to the right when traversing the bounding loops in the positive sense.
For curves on surface the reference_to_curve will be unaffected by any transformation.
The cartesian_transformation_operator shall only be applied to geometry defined in a consistent system of units with the same units on each axis. With all optional attributes omitted, the transformation defaults to the identity transformation. The cartesian_transformation_operator shall only be instantiated as one of its subtypes.
NOTE See Figures (4a) to (4c) for demonstration of effect of transformation.
EXPRESS specification:
*)
ENTITY cartesian_transformation_operator
SUPERTYPE OF (ONEOF (cartesian_transformation_operator_2d,
cartesian_transformation_operator_3d))
SUBTYPE OF (geometric_representation_item, functionally_defined_transformation);
axis1 :
OPTIONAL
direction;
axis2 :
OPTIONAL
direction;
local_origin : cartesian_point;
scale :
OPTIONAL
REAL;
DERIVE
scl : REAL := NVL(scale, 1.0);
WHERE
WR1: scl > 0.0;
END_ENTITY;
(*
Attribute definitions:
axis1: the direction used to determine u[1], the derived X axis direction;
axis2: the direction used to determine u[2], the derived Y axis direction;
local_origin: the required translation, specified as a cartesian point. The actual translation included in the transformation is from the geometric origin to the local origin;
scale: the scaling value specified for the transformation;
scl: the derived scale S of the transformation, equal to scale if that exists, or 1.0 otherwise.
Formal propositions:
WR1: The derived scaling factor scl shall be greater than zero.

EXPRESS specification:
*)
ENTITY cartesian_transformation_operator_3d
SUBTYPE OF (cartesian_transformation_operator);
axis3 :
OPTIONAL
direction;
DERIVE
u : LIST[3:3] OF direction := base_axis(3,SELF\cartesian_transformation_operator.axis1, SELF\cartesian_transformation_operator.axis2,axis3);
WHERE
WR1: SELF\geometric_representation_item.dim = 3;
END_ENTITY;
(*
Attribute definitions:
axis3: the exact direction of u[3], the derived Z axis direction;
u: the list of mutually orthogonal, normalised vectors defining the transformation matrix T. They are derived from the explicit attributes axis3, axis1, and axis2 in that order;
Formal propositions:
WR1: The coordinate space dimensionality shall be 3.

EXPRESS specification:
*)
ENTITY cartesian_transformation_operator_2d
SUBTYPE OF (cartesian_transformation_operator);
DERIVE
u : LIST[2:2] OF direction := base_axis(2,SELF\cartesian_transformation_operator.axis1, SELF\cartesian_transformation_operator.axis2,?);
WHERE
WR1: SELF\geometric_representation_item.dim = 2;
END_ENTITY;
(*
Attribute definitions:
u: the list of mutually orthogonal, normalised vectors defining the transformation matrix T. They are derived from the explicit attributes axis1, and axis2 in that order;
Formal propositions:
WR1: The coordinate space dimensionality shall be 2.

EXPRESS specification:
*)
ENTITY curve
SUPERTYPE OF (ONEOF (line,
conic,
clothoid,
circular_involute,
pcurve,
surface_curve,
offset_curve_2d,
offset_curve_3d,
curve_replica))
SUBTYPE OF (geometric_representation_item);
END_ENTITY;
(*
Informal propositions:
IP1: A curve shall be arcwise connected.
IP2: A curve shall have an arc length greater than zero.
IP3: Where definitions of curve parameterisation are not defined in parametric or geometric terms, a curve shall be assumed by default to have arc length parameterisation.
NOTE 1 IP3 is based on the "Fundamental concepts and assumptions" in clause 4.2, in particular, "4.2.3 Parametrisation of analytic curves and surfaces".

A line is a type of curve, that is an unbounded with constant tangent direction. A line is defined by a point and a direction. The positive direction of the line is in the direction of the dir vector.
The curve is parametrised as follows:
P = pnt
V = dir
λ (u) = P + u V
and the parametric range is -∞ < u < ∞.
EXPRESS specification:
*)
ENTITY line
SUBTYPE OF (curve);
pnt : cartesian_point;
dir : vector;
WHERE
WR1: dir.dim = pnt.dim;
END_ENTITY;
(*
Attribute definitions:
pnt: the location of the line;
dir: the direction of the line; the magnitude and units of dir affect the parametrisation of the line;
Formal propositions:
WR1: The attributes pnt and dir shall both be 2D or both be 3D entities.

A conic is a type of curve, that is a planar curve which could be produced by intersecting a plane with a cone.
A conic is defined in terms of its intrinsic geometric properties rather than being described in terms of other geometry.
A conic entity always has a placement coordinate system defined by axis2_placement; the parametric representation is defined in terms of this placement coordinate system.
EXPRESS specification:
*)
ENTITY conic
SUPERTYPE OF (ONEOF (circle,
ellipse,
hyperbola,
parabola))
SUBTYPE OF (curve);
position : axis2_placement;
END_ENTITY;
(*
Attribute definitions:
position: the location and orientation of the conic. Further details of the interpretation of this attribute are given for the individual subtypes.

A circle is a type of conic, section defined by a radius and the location and orientation of the circle.
Interpretation of the data shall be as follows:
C = position.location (centre)
x = position.p[1]
y = position.p[2]
z = position.p[3]
R = radius
The circle is parametrised as follows:
λ (u) = C +R(cos(u)x + sin(u)y)
and the parametric range is 0 ≤ u ≤ 360 degrees, u is an angular parameter and when a numerical value is specified it shall use the current units for plane_angle_measure.
In the placement coordinate system defined above, the circle has the equation C = 0, where
C (x, y, z) = x2 + y2 - R2
The positive sense of the circle at any point is in the tangent direction, T, to the curve at the point, where
T =(-C y, C x, 0).
NOTE 1 A circular arc is defined by using the trimmed_curve entity in conjunction with the circle entity.
EXPRESS specification:
*)
ENTITY circle
SUBTYPE OF (conic);
radius : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
radius: the radius of the circle, which shall be greater than zero;
NOTE 2 See Figure (5) for interpretation of attributes.

An ellipse is a type of conic, section defined by the lengths of the semi-major and semi-minor diameters and the position (center or mid point of the line joining the foci) and orientation of the curve.
Interpretation of the data shall be as follows:
C = position.location (centre)
x = position.p[1]
y = position.p[2]
z = position.p[3]
R1 = semi_axis_1
R2 = semi_axis_2
The ellipse is parametrised as follows:
λ (u) = C +R1(cos(u)x) + R1( sin(u)y)
and the parametric range is 0 ≤ u ≤ 360 degrees, u is an angular parameter and when a numerical value is specified it shall use the current units for plane_angle_measure.
In the placement coordinate system defined above, the ellipse has the equation C = 0, where
C (x, y, z) = {x/(R1)}2 + {y/(R2)}2 - 1
The positive sense of the ellipse at any point is in the tangent direction, T, to the curve at the point, where
T =(-C y, C x, 0).
EXPRESS specification:
*)
ENTITY ellipse
SUBTYPE OF (conic);
semi_axis_1 : positive_length_measure;
semi_axis_2 : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
semi_axis_1: the first radius of the ellipse which shall be positive.
semi_axis_2: the second radius of the ellipse which shall be positive.
NOTE See Figure (6) for interpretation of attributes.

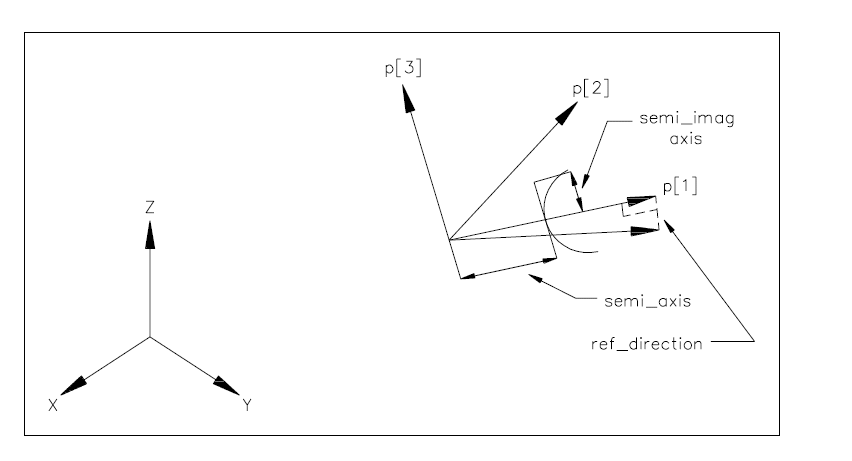
An hyperbola is a type of conic, section defined by the lengths of the major and minor radii and the position (mid-point of the line joining two foci) and orientation of the curve. Interpretation of the data shall be as follows:
C = position.location (centre)
x = position.p[1]
y = position.p[2]
z = position.p[3]
R1 = semi_axis
R2 = semi_imag_axis
The hyperbola is parametrised as follows:
λ (u) = C +R1(cosh(u))x + R2( sinh(u))y
The parametrisation range is -∞ < (u) < ∞
In the placement coordinate system defined above, the hyperbola has the equation C = 0, where
C (x, y, z) = (x/R1)2 - (y/R2)2 - 1
The positive sense of the hyperbola at any point is in the tangent direction, T, to the curve at the point, where
T =(-C y, C x, 0).
The branch of the hyperbola represented is that pointed to by the x direction.
EXPRESS specification:
*)
ENTITY hyperbola
SUBTYPE OF (conic);
semi_axis : positive_length_measure;
semi_imag_axis : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
semi_axis: the length of the semi-axis of the hyperbola. This is positive and is half the minimum distance between the two branches of the hyperbola.
semi_imag_axis: the length of the semi-imaginary axis of the hyperbola which shall be positive;
NOTE See Figure (7) for interpretation of attributes.

A parabola is a type of conic, section defined by its focal length, position (apex), and orientation. Interpretation of the data shall be as follows:
C = position.location (centre)
x = position.p[1]
y = position.p[2]
z = position.p[3]
F = focal_dist
The parabola is parametrised as follows:
λ (u) = C + F(u2 x + 2u y)
The parametrisation range is -∞ < (u) < ∞
In the placement coordinate system defined above, the parabola has the equation C = 0, where
C (x, y, z) = 4Fx - y2
The positive sense of the parabola at any point is in the tangent direction, T, to the curve at the point, where
T =(-C y, C x, 0).
EXPRESS specification:
*)
ENTITY parabola
SUBTYPE OF (conic);
focal_dist : length_measure;
WHERE
WR1: focal_dist <> 0.0;
END_ENTITY;
(*
Attribute definitions:
focal_dist: the distance of the focal point from the apex point;
NOTE See Figure (8) for interpretation of attributes.
Formal propositions:
WR1: The focal distance shall not be zero.

A clothoid is a type of curve, and is a planar curve in the form of a spiral. This curve has the property that the curvature varies linearly with the arc length. Interpretation of the data shall be as follows:
C = position.location (centre)
x = position.p[1]
y = position.p[2]
C = clothoid_constant
The clothoid is parametrised as follows:
λ (u) = C + A√{π}(∫0 u cos(π(t2/2))dt x + ∫0 u sin(π(t2/2))dt y
The parametrisation range is -∞ < u < ∞
The arc length s of the curve, from the point C, is given by the formula: s = A u√π.
The curvature κ and radius of curvature ρ, at any point of the curve, are related to the arc length by the formulae:
ρ = s/(A2) , ρ = 1/κ.
NOTE 1 A more detailed description of the clothoid curve can be found in GIBSON[8].
EXPRESS specification:
*)
ENTITY clothoid
SUBTYPE OF (curve);
position : axis2_placement;
clothoid_constant : length_measure;
END_ENTITY;
(*
Attribute definitions:
position: the location and orientation of the clothoid;
location is the point on the clothoid with zero curvature.
position.p[1] is the direction of the tangent to the curve at this point.
NOTE 2 If position is of type axis2_placement_2d the clothoid is defined in a two dimensional space.
NOTE 3 See Figure (9) for interpretation of attributes.
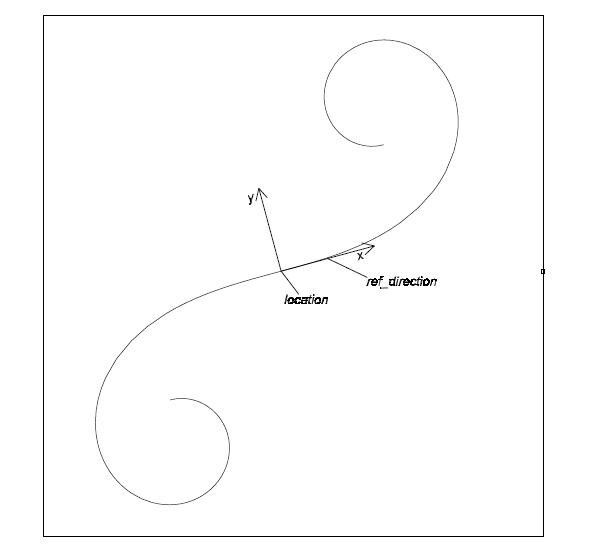
clothoid_constant: the constant which defines the relationship between curvature and arc length for the curve;

A circular_involute is a type of curve, and is the involute of a circle. The involute of a planar curve is the locus of the end point of a thread as it is wound round the curve. If P0 is the point where the involute meets the circle the distance from any point P on the involute to the tangential contact point T on the circle is equal to the arc length from P0 to T. The circular_involute has a cusp at the point P0 (u = 0), and forms a double spiral enclosing the base circle.
NOTE 1 See GIBSON[9] for further properties of involute curves.
Interpretation of the data shall be as follows:
C = position.location (centre)
x = position.p[1]
y = position.p[2]
r = base_radius
The circular_involute is parametrised as follows:
λ (u) = C + r( cos(u) + usin(u))x + r( sin(u) - ucos(u))y
The parameter u is measured in radians and parametrisation range is -∞ < (u) < ∞
The arc length s of the curve, from the point u = 0 , is given by the formula: s =(1/2) r u2
At any point on the involute the distance PC from a point P on the curve with parameter u to the centre point C satisfies the equation:
(PC) 2 = r2(1 + u2)
NOTE 2 See Figure (10) 10 for the interpretation of the attributes. This figure shows a portion of the curve for parameter values between -1.5 and +1.5.
EXPRESS specification:
*)
ENTITY circular_involute
SUBTYPE OF (curve);
position : axis2_placement;
base_radius : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
position: the location and orientation of the circular_involute;
position.location the the centre C of the base circle from which the involute is defined.
position.p[1] The direction from centre of the base circle to the cusp point P0 of the circular_involute.
base_radius:
the radius of the base circle, for which the
circular_involute is the wrapping curve.
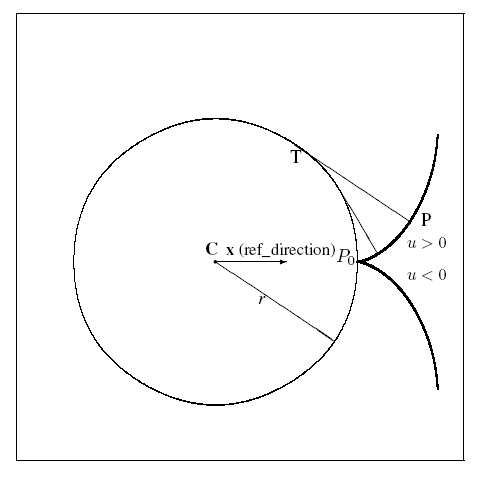

A bounded_curve is a type of curve of finite arc length with identifiable end points.
NOTE A bounded_curve is not included in the ONEOF list for curve and, as such, has an implicit and/or relationship with other subtypes of curve. The only complex instances intended to be created are bounded_pcurve and bounded_surface_curve.
EXPRESS specification:
*)
ENTITY bounded_curve
SUPERTYPE OF (ONEOF (polyline,
b_spline_curve,
trimmed_curve,
bounded_pcurve,
bounded_surface_curve,
composite_curve,
locally_refined_spline_curve))
SUBTYPE OF (curve);
END_ENTITY;
(*
Informal propositions:
IP1: A bounded curve has finite arc length.
IP2: A bounded curve has a start point and an end point.

A polyline is a type of bounded_curve with (n-1) linear segments, defined by a list of n cartesian_point s,
P1, P2, ..... , Pn.
The ith segment of the curve is parametrised as follows:
λ (u) = P i(i-u) + P i+1(u+1-i), for 1 ≤ i ≤ n-1
where i-1 ≤ u ≤ i and with parametric range of 0 ≤ u ≤ n-1.
EXPRESS specification:
*)
ENTITY polyline
SUBTYPE OF (bounded_curve);
points : LIST[2:?] OF cartesian_point;
END_ENTITY;
(*
Attribute definitions:
points: the cartesian_points defining the polyline;

A b_spline_curve is a type of bounded_curve, it is a piecewise parametric polynomial or rational curve described in terms of control points and basis functions. The B-spline curve has been selected as the most stable format to represent all types of polynomial or rational parametric curves. With appropriate attribute values it is capable of representing single span or spline curves of explicit polynomial, rational, Bézier or B-spline type. The b_spline_curve has three special subtypes where the knots and knot multiplicities can be derived to provide simple default capabilities.
NOTE 1 Identification of B-spline curve default values and subtypes is important for performance considerations and for efficiency issues in performing computations.
NOTE 2 A B-spline is rational if and only if the weights are not all identical; this can be represented by the rational_b_spline_curve subtype. If it is polynomial, the weights may be defaulted to all being 1.
NOTE 3 In the case where the B-spline curve is uniform, quasi-uniform or Bézier (including piecewise Bézier), the knots and knot multiplicities may be defaulted (i.e., non-existent in the data as specified by the attribute definitions).
NOTE 4 When the knots are defaulted, a difference of 1.0 between separate knots is assumed, and the effective parameter range for the resulting curve starts from 0.0. These defaults are provided by the subtypes.
NOTE 5 The knots and knot multiplicities shall not be defaulted in the non-uniform case.
NOTE 6 The defaulting of weights and knots are done independently of one another.
NOTE 7 Definitions of the B-spline basis functions Ni d,(u) can be found in [5], [8], [11] and [12]. It should be noted that there is a difference in terminology between these references.
Interpretation of the data shall be as follows:
a) The curve, in the polynomial case, is given by:
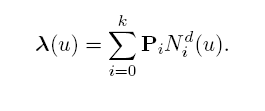
b) In the rational case all weights shall be positive and the curve is given by:
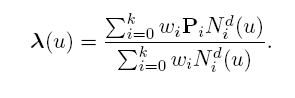
where
k+1 = number of control points
P i = control points
wi = weights, and
d = degree.
The knot array is an array of (k + d + 2) real numbers [u-d,.. ,uk+1], such that for all indices j in [-d, k], uj ≤ uj+1 . This array is obtained from the knots list by repeating each multiple knot according to the multiplicity. Ni d , the ith normalised B-spline basis function of degree d, is defined on the subset [ui-d, ... ,ui+1] of this array.
c) Let L denote the number of distinct values amongst the d + k +2 knots in the knot list; L will be referred to as the `upper index on knots'. Let mj denote the multiplicity (i.e., number of repetitions) of the jth distinct knot. Then:
ΣL i=1 mi = d + k + 2.
All knot multiplicities except the first and the last shall be in the range 1, . . . , d; the first and last may have a maximum value of d + 1.
NOTE 8 In evaluating the basis functions, a knot u of, for example, multiplicity 3 is interpreted as a sequence u, u, u, in the knot array.
The b_spline_curve has three special subtypes where the knots and knot multiplicities are derived to provide simple default capabilities.NOTE 9 See Figure (11) for further information on curve definition.
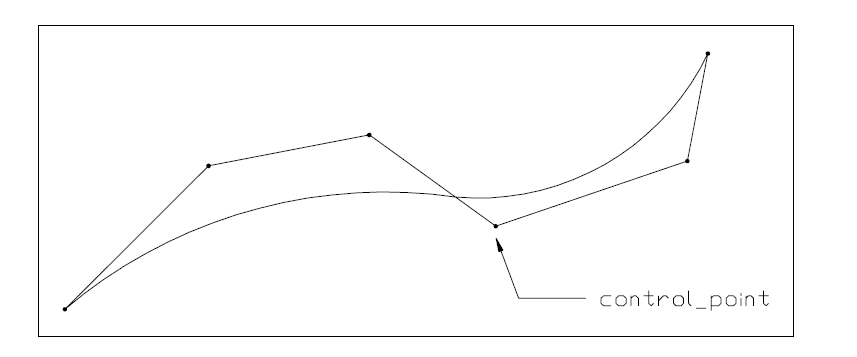
EXPRESS specification:
*)
ENTITY b_spline_curve
SUPERTYPE OF (ONEOF (uniform_curve,
b_spline_curve_with_knots,
quasi_uniform_curve,
bezier_curve)
ANDOR rational_b_spline_curve)
SUBTYPE OF (bounded_curve);
degree : INTEGER;
control_points_list : LIST[2:?] OF cartesian_point;
curve_form : b_spline_curve_form;
closed_curve : LOGICAL;
self_intersect : LOGICAL;
DERIVE
upper_index_on_control_points : INTEGER := (SIZEOF(control_points_list) - 1);
control_points : ARRAY[0:upper_index_on_control_points] OF cartesian_point := list_to_array(control_points_list,0, upper_index_on_control_points);
WHERE
WR1: ('GEOMETRY_SCHEMA.UNIFORM_CURVE' IN TYPEOF(self)) OR ('GEOMETRY_SCHEMA.QUASI_UNIFORM_CURVE' IN TYPEOF(self)) OR ('GEOMETRY_SCHEMA.BEZIER_CURVE'
IN TYPEOF(self)) OR ('GEOMETRY_SCHEMA.B_SPLINE_CURVE_WITH_KNOTS' IN TYPEOF(self));
END_ENTITY;
(*
Attribute definitions:
degree: the algebraic degree of the basis functions;
control_points_list: the list of control points for the curve;
curve_form: used to identify particular types of curve; it is for information only;
closed_curve: indication of whether the curve is closed; it is for information only;
NOTE 10 > Where part of the data is described as `for information only' this implies that if there is any discrepancy between this information and the properties derived from the curve itself, the curve data takes precedence.
self_intersect: flag to indicate whether the curve self-intersects or not; it is for information only;
upper_index_on_control_points: the upper index on the array of control points; the lower index is 0, this value is derived from the control_points_list;
control_points: the array of control points used to define the geometry of the curve; this is derived from the list of control points.
Formal propositions:
WR1: Any instantiation of this entity shall include one of the subtypes b_spline_curve_with_knots uniform_curve, quasi_uniform_curve or bezier_curve.

A b_spline_curve_with_knots is a type of b_spline_curve, for which the knot values are explicitly given. This subtype shall be used to represent non-uniform B-spline curves and may be used for other knot types.
Let L denote the number of distinct values amongst the d + k +2 knots in the knot list; L will be referred to as the `upper index on knots'. Let mj denote the multiplicity (i.e., number of repetitions) of the jth distinct knot. Then:
Σ i=1 L mi = d + k + 2.
All knot multiplicities except the first and the last shall be in the range 1, . . ., d; the first and last may have a maximum value of d + 1.
NOTE 1 In evaluating the basis functions, a knot u of, for example, multiplicity 3 is interpreted as a sequence u, u, u, in the knot array.
EXPRESS specification:
*)
ENTITY b_spline_curve_with_knots
SUBTYPE OF (b_spline_curve);
knot_multiplicities : LIST[2:?] OF INTEGER;
knots : LIST[2:?] OF parameter_value;
knot_spec : knot_type;
DERIVE
upper_index_on_knots : INTEGER := SIZEOF(knots);
WHERE
WR1: constraints_param_b_spline(degree, upper_index_on_knots, upper_index_on_control_points, knot_multiplicities, knots);
WR2: SIZEOF(knot_multiplicities) = upper_index_on_knots;
END_ENTITY;
(*
Attribute definitions:
knot_multiplicities: the multiplicities of the knots; this list defines the number of times each knot in the knots list is to be repeated in constructing the knot array;
knots: the list of distinct knots used to define the B-spline basis functions;
knot_spec: the description of the knot type; this is for information only;
NOTE 2 Where part of the data is described as `for information only' this implies that if there is any discrepancy between this information and the properties derived from the curve itself, the curve data takes precedence.
upper_index_on_knots: the upper index on the knot arrays; the lower index is 1;
Formal propositions:
WR1: The function constraints_param_b_spline returns TRUE if no inconsistencies in the parametrisation of the B-spline are found.
WR2: The number of elements in the knot multiplicities list shall be equal to the number of elements in the knots list.

A uniform_curve is a type of b_spline_curve, in which the knots are evenly spaced. Suitable default values for the knots and knot multiplicities are derived in this case. A B-spline is uniform if and only if all knots are of multiplicity 1 and they differ by a positive constant from the preceding knot. In this subtype the knot spacing is 1.0, starting at -d, where d is the degree.
NOTE 1 If the B-spline curve is uniform and degree = 1, the B-spline is equivalent to a polyline
NOTE 2 The value k_up may be required for the upper index on the knot and knot multiplicity lists. This is computed from the degree and the number of control points.
k_up = SELF\b_spline_curve.upper_index_on_control_points + degree + 2.
If required, the knots and knot multiplicities can be computed by the function calls:
default_b_spline_knots(SELF\b_spline_curve.degree, k_up,uniform_knots),
default_b_spline_knot_mult(SELF\b_spline_curve.degree,k_up, uniform_knots).
EXPRESS specification:
*)
ENTITY uniform_curve
SUBTYPE OF (b_spline_curve);
END_ENTITY;
(*

A quasi_uniform_curve is a type of b_spline_curve, in which the knots are evenly spaced, and except for the first and last, have multiplicity 1. Suitable default values for the knots and knot multiplicities are derived in this case. A B-spline is quasi-uniform if and only if the knots are of multiplicity (degree+1) at the ends, of multiplicity 1 elsewhere, and they differ by a positive constant from the preceding knot. A quasi-uniform B-spline curve which has only two knots represents a Bézier curve. In this subtype the knot spacing is 1.0, starting at 0.0.
NOTE The value k_up may be required for the upper index on the knot and knot multiplicity lists. This is computed from the degree and the number of control points.
k_up = SELF\b_spline_curve.upper_index_on_control_points + degree + 2.
If required, the knots and knot multiplicities can be computed by the function calls:
default_b_spline_knots (SELF\b_spline_curve.degree, k_up,quasi_uniform_knots),
default_b_spline_knot_mult (SELF\b_spline_curve.degree,k_up, quasi_uniform_knots).
EXPRESS specification:
*)
ENTITY quasi_uniform_curve
SUBTYPE OF (b_spline_curve);
END_ENTITY;
(*

A bezier_curve is a type of b_spline_curve, that represents in the most general case a piecewise Bézier curve. This is a special type of curve which can be represented as a type of b_spline_curve in which the knots are evenly spaced and have high multiplicities. Suitable default values for the knots and knot multiplicities are derived in this case.
A B-spline curve is a piecewise Bézier curve if it is quasi-uniform except that the interior knots have multiplicity degree rather than having multiplicity one. In this subtype the knot spacing is 1.0, starting at 0.0. A piecewise Bézier curve which has only two knots, 0.0 and 1.0, each of multiplicity (degree+1), is a simple Bézier curve.
NOTE 1 A simple Bézier curve can be defined as a B-spline curve with knots by the following data:
degree = (d)
upper index on control points (equal to d)
control points (d + 1 cartesian points)
knot type (equal to quasi-uniform knots)
knot multiplicities = (d+1, d+1)
knots = (0.0, 1.0)
No other data are needed, except for a rational Bézier curve. In this case the weights data ((d + 1) REALs) shall be given.
NOTE 2 It should be noted that every piecewise Bézier curve has an equivalent representation as a B-spline curve. Because of problems with non-uniform knots not every B-spline curve can be represented as a piecewise Bézier curve., To define a piecewise Bézier curve as a B-spline:
The first knot is 0.0 with multiplicity (d + 1).
The next knot is 1.0 with multiplicity d
(the knots for one segment are now defined, unless it is the last one).
The next knot is 2.0 with multiplicity d (the knots for two segments are now defined, unless the second is the last one).
Continue to the end of the last segment, call it the n-th segment, at the end of which a knot with value n, multiplicity (d + 1) is added.
EXAMPLE 1 A one-segment cubic Bézier curve would have knot sequence (0,1) with multiplicity sequence (4,4).
EXAMPLE 2 A two-segment cubic piecewise Bézier curve would have knot sequence (0,1,2) with multiplicity sequence (4,3,4).
NOTE 3 For the piecewise Bézier case, if d is the degree, k+1 is the number of control points, m is the number of knots with multiplicity d, and N is the total number of knots for the spline, then
(d + 2 + k) = N = (d + 1) + md + (d + 1)
thus, m = (k - d)/d
Thus, the knot sequence is (0, 1, ..., m, (m+1)) with multiplicities (d+1, d,. . ., d, d+1).
NOTE 3 The value k_up may be required for the upper index on the knot and knot multiplicity lists. This is computed from the degree and the number of control points.
k_up = (SELF\backslash b_spline_curve.upper_index_on_control_points)/(SELF\backslash b_spline_curve.degree + 1)
If required, the knots and knot multiplicities can be computed by the function calls:
default_b_spline_knots(SELF\b_spline_curve.degree, k_up, piecewise_bezier_knots),
default_b_spline_knot_mult(SELF\b_spline_curve.degree,k_up, piecewise_bezier_knots).
EXPRESS specification:
*)
ENTITY bezier_curve
SUBTYPE OF (b_spline_curve);
END_ENTITY;
(*

A rational_b_spline_curve is a type of b_spline_curve, that is a piecewise parametric rational curve described in terms of control points and basis functions. This subtype is instantiated with one of the other subtypes of b_spline_curve which explicitly or implicitly provide the knot values used to define the basis functions.
All weights shall be positive and the curve is given by:
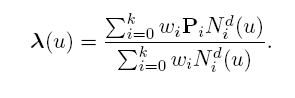
EXPRESS specification:
*)
ENTITY rational_b_spline_curve
SUBTYPE OF (b_spline_curve);
weights_data : LIST[2:?] OF REAL;
DERIVE
weights : ARRAY[0:upper_index_on_control_points] OF REAL := list_to_array(weights_data,0, upper_index_on_control_points);
WHERE
WR1: SIZEOF(weights_data) = SIZEOF(SELF\b_spline_curve. control_points_list);
WR2: curve_weights_positive(SELF);
END_ENTITY;
(*
Attribute definitions:
weights_data: the supplied values of the weights; see the derived attribute weights;
weights: the array of weights associated with the control points. This is derived from the weights_data;
Formal propositions:
WR1: There shall be the same number of weights as control points.
WR2: All the weights shall have values greater than 0.0.

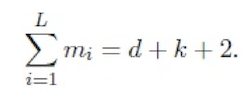
EXPRESS specification:
*)
ENTITY local_b_spline
SUBTYPE OF (representation_item);
degree : INTEGER;
knots : LIST[2:?] OF INTEGER;
multiplicities : LIST[2:?] OF INTEGER;
WHERE
WR1: degree > 0;
WR2: SIZEOF(knots) = SIZEOF(multiplicities);
WR3: constraints_param_local_b_spline(degree, knots, multiplicities);
END_ENTITY;
(*
Attribute definitions:
degree: the polynomial degree of the local_b_spline;
knots: the list of pointers to the distinct knot values in increasing order;
multiplicities: the list of positive integers defining the multiplicities of the knots.
Formal propositions:
WR1: The degree shall be positive;
WR2: The number of knots shall be equal to the number of multiplicities;
WR3: The values of the knots and multiplicities shall be compatible with the degree and the continuity requirements for a B-spline function. The function constraints_param_local_b_spline applies the following tests:
the sum of knot multiplicities = degree + 2,
for the first and last knot the multiplicity is bounded by 1 and (degree+1),
for all other knots the knot multiplicity is bounded by 1 and degree.
the consecutive knots are increasing in value.

A locally_refined_spline_curve is a type of bounded_curve that is a piecewise parametric polynomial or rational curve described in terms of control points and local B-spline functions. If the set of B-spline functions are linearly independent, they will form a basis. With appropriate attribute values, the curve is capable of representing single span or spline curves of explicit polynomial, rational, Bézier or B-spline type. Furthermore, the degree of the curve can vary as the B-splines from which it is defined, need not to have the same polynomial degree.
NOTE 1 A locally refined spline curve is rational if and only if the weights are not all identical; this can be represented by the rational_locally_refined_spline_curve subtype. If it is polynomial, the weights may be defaulted to all being 1.
Interpretation of the data is as follows: The curve, in the polynomial case, is given by:
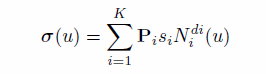
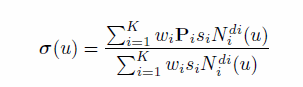
where
K = number of control points,
P i = control points,
si = scaling_factors(i),
wi = weights_data(i),
N i = local B-splines, and
di=degree.
NOTE 2 The degree is associated with the local B-spline and does not need to be constant throughout the curve.
The knot values are defined in the spline_knot_values type, and the knot multiplicity is defined in the entity local_b_spline.NOTE 3 When the polynomial degree is the same for all B-splines and no knot lines exist that do not cross the entire parameter domain, the locally_refined_spline_curve will coincide with b_spline_curve_with_knots. In that case b_spline_curve_with_knots has the simplest and most compact representation.
NOTE 4 A locally_refined_spline_curve can be of type analysis suitable T-spline, hierarchical B-spline, LR-spline, semi standard T-spline or standard T-spline. The type is given by the enumeration locally_refined_spline_type_enum, and the packing and unpacking of the curve will depend on this type.
EXPRESS specification:
*)
ENTITY locally_refined_spline_curve
SUBTYPE OF (bounded_curve);
b_splines : LIST[2:?] OF local_b_spline;
knot_values : spline_knot_values;
control_points_list : LIST[2:?] OF cartesian_point;
scaling_factors : LIST[2:?] OF REAL;
closed_curve : LOGICAL;
locally_refined_spline_type : locally_refined_spline_type_enum;
self_intersect : LOGICAL;
domain : LIST[2:2] OF REAL;
WHERE
WR1: SIZEOF(b_splines) = SIZEOF(control_points_list);
WR2: SIZEOF(scaling_factors) = SIZEOF(control_points_list);
WR3: constraints_scaling(scaling_factors);
END_ENTITY;
(*
Attribute definitions:
b_splines: the local B-spline functions from which the curve is defined. If they are linearly independent, the set of B-splines will form a basis. The b_splines and consequently also the control_points_list and scaling_factors, are ordered according to the first knot in the local B-spline function. In case of ambiguities, the sorting factors are the last knot in the B-spline function and finally the multiplicity of the first knot.
knot_values: the list of distinct knot values;
control_points_list: the list of control points;
scaling_factors: the list of scaling factors, these factors are used to ensure that the non-zero B-splines at all points in the domain add up to unity (partition of unity). LR B-splines, hierarchical B-splines and some variants of T-splines ensure partition of unity by scaling. Other variants of T-splines use rational scaling.
closed_curve: indication whether the curve is closed; this is for information only;
locally_refined_spline_type: the type of the initial locally refined spline curve that provides rules for how the stored curve can be unpacked to its original format;
self_intersect: indication whether the curve is self-intersecting; this is for information only;
domain: the parameter domain corresponding to the curve. domain(1) is the minimum parameter value , domain(2) is the maximum parameter value. If the B-splines at the ends have a knot multiplicity equal to the degree+1, the domain will coincide with the domain given by the minimum and maximum values in knot_values. Otherwise, it will be coincide with a domain given by nearby knots depending on knot multiplicities. Otherwise, it will be coincide with a domain given by nearby knots depending upon knot multiplicities.
Formal propositions:
WR1: the size of the b_splines list shall be equal to the number of control points;
WR2: the number of scaling_factors shall be equal to the number of control points.
WR3: all scaling_factors shall be positive and not greater than 1.0.

A rational_locally_refined_spline_curve is a type of locally_refined_spline_curve that is a piecewise parametric rational curve described in terms of control points and local B-spline functions.
EXPRESS specification:
*)
ENTITY rational_locally_refined_spline_curve
SUBTYPE OF (locally_refined_spline_curve);
weights_data : LIST[2:?] OF REAL;
WHERE
WR1: SIZEOF(weights_data) = SIZEOF(SELF\locally_refined_spline_curve.
control_points_list);
WR2: weights_positive(weights_data);
END_ENTITY;
(*
Attribute definitions:
weights_data: the supplied values of the weights.
Formal propositions:
WR1: the size of the of weights_data list shall be equal to the number of control points
WR2: all values in the weights_data list shall be positive.

A trimmed_curve is a type of bounded_curve, which is created by taking a selected portion, between two identified points, of the associated basis curve. The basis curve itself is unaltered and more than one trimmed curve may reference the same basis curve. Trimming points for the curve may be identified:
by parametric value;
by geometric position;
by both of the above.
At least one of these shall be specified at each end of the curve. The sense makes it possible to unambiguously define any segment of a closed curve such as a circle. The combinations of sense and ordered end points make it possible to define four distinct directed segments connecting two different points on a circle or other closed curve. For this purpose cyclic properties of the parameter range are assumed; for example, 370 degrees is equivalent to 10 degrees. The trimmed curve has a parametrisation which is inherited from that of the particular basis curve referenced. More precisely the parameter s of the trimmed curve is derived from the parameter t of the basis curve as follows:
If sense is TRUE: s = t - t1.
If sense is FALSE: s = t1 - t.
In the above equations t1 is the value given by trim_1 or the parameter value corresponding to point_1 and t2 is the parameter value given by trim_2 or the parameter corresponding to point_2. The resultant trimmed curve has a parameter s ranging from 0 at the first trimming point to |t2 - t1| at the second trimming point.
NOTE 1 In the case of a closed basis curve, it may be necessary to increment 1 or 2 by the parametric length for consistency with the sense flag.
NOTE 2 For example:
(a) If sense_agreement = TRUE and t2 < t1, t2 should be increased by the parametric length.
(b) If sense_agreement = FALSE and t1 > t2 , t1 should be increased by the parametric length.
EXPRESS specification:
*)
ENTITY trimmed_curve
SUBTYPE OF (bounded_curve);
basis_curve : curve;
trim_1 : SET[1:2] OF trimming_select;
trim_2 : SET[1:2] OF trimming_select;
sense_agreement : BOOLEAN;
master_representation : trimming_preference;
WHERE
WR1: (HIINDEX(trim_1) = 1) OR (TYPEOF(trim_1[1]) <> TYPEOF(trim_1[2]));
WR2: (HIINDEX(trim_2) = 1) OR (TYPEOF(trim_2[1]) <> TYPEOF(trim_2[2]));
END_ENTITY;
(*
Attribute definitions:
basis_curve: the curve to be trimmed. For curves with multiple representations any parameter values given as trim_1 or trim_2 refer to the master representation of the basis_curve only;
trim_1: the first trimming point which may be specified as a cartesian_point (point_1), as a real parameter value (parameter_1 = t1 ), or both;
trim_2: the second trimming point which may be specified as a cartesian_point (point_2), as a real parameter value (parameter_2 = t2 ), or both;
sense_agreement: flag to indicate whether the direction of the trimmed curve agrees with or is opposed to the direction of basis_curve.
sense_ agreement = TRUE if the curve is being traversed in the direction of increasing parametric value;
sense_agreement =FALSE otherwise.
For an open curve, sense_agreement = FALSE if t1 > t2 .
If t2 >t1 , sense_agreement = TRUE.
The sense information is redundant in this case but is essential for a closed curve.
master_representation: where both parameter and point are present at either end of the curve this indicates the preferred form. Multiple representations provide the ability to communicate data in more than one form, even though the data are expected to be geometrically identical.
NOTE 3 The master_representation attribute acknowledges the impracticality of ensuring that multiple forms are indeed identical and allows the indication of a preferred form. This would probably be determined by the creator of the data. All characteristics, such as parametrisation, domain, and results of evaluation, for an entity having multiple representations, are derived from the master representation. Any use of the other representations is a compromise for practical considerations.
Formal propositions:
WR1: Either a single value is specified for trim_1, or, the two trimming values are of different types (point and parameter).
WR2: Either a single value is specified for trim_2, or, the two trimming values are of different types (point and parameter).
Informal propositions:
IP1: Where both the parameter value and the cartesian point exist for trim_1 or trim_2 they shall be consistent, i.e., the basis_curve evaluated at the parameter value shall coincide with the specified point.
IP2: When a cartesian point is specified by trim_1 or by trim_2, it shall lie on the basis_curve.
IP3: Except in the case of a closed basis_curve, where both parameter_1 and parameter_2 exist, they shall be consistent with the sense flag, i.e., sense = (parameter_1 < parameter_2).
IP4: If both parameter_1 and parameter_2 exist, (parameter_1 < > parameter_2).
IP5: When a parameter value is specified by trim_1 or trim_2, it shall lie within the parametric range of the basis_curve.

A composite_curve is a type of bounded_curve, that is a collection of curves joined end-to-end. The individual segments of the curve are themselves defined as composite_curve_segments. The parametrisation of the composite curve is an accumulation of the parametric ranges of the referenced bounded curves. The first segment is parametrised from 0 to l1 , and, for i ≥ 2, the i th segment is parametrised from
where lk is the parametric length (i.e., difference between maximum and minimum parameter values) of the curve underlying the k th segment.
Let T denote the parameter for the composite_curve.
Then, if the ith segment is not a reparametrised_composite_curve_segment, T is related to the parameter t1, ti0, ≤ t1, ≤ ti1 for the ith segment by the equation:
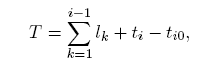
if segments[i].same_sense = TRUE;
or by the equation:
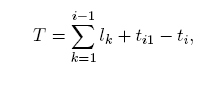
if segments[i].same_sense = FALSE.
If segments[i] is of type reparametrised_composite_curve_segment,
T = Σk=1 i-1 lk + τ
Where τ is defined in reparametrised_composite_curve_segment.
NOTE See Figure (13) for further information on curve definition and attributes.
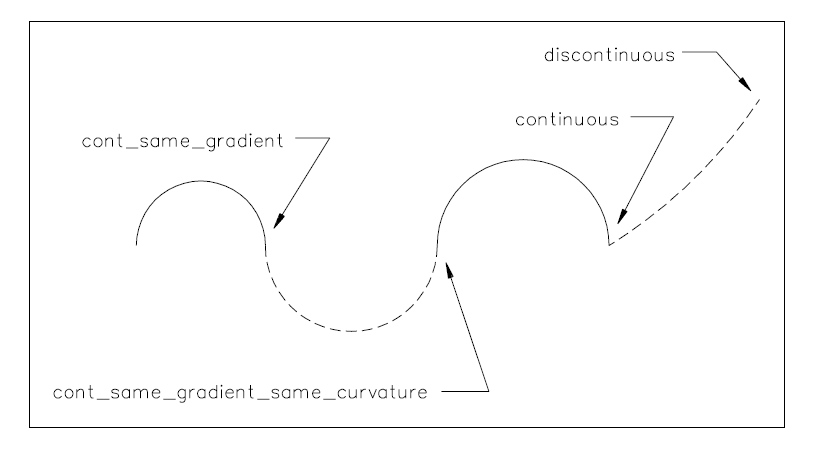
EXPRESS specification:
*)
ENTITY composite_curve
SUBTYPE OF (bounded_curve);
segments : LIST[1:?] OF composite_curve_segment;
self_intersect : LOGICAL;
DERIVE
n_segments : INTEGER := SIZEOF(segments);
closed_curve : LOGICAL := segments[n_segments].transition <> discontinuous;
WHERE
WR1: ((NOT closed_curve) AND (SIZEOF(QUERY(temp <* segments | temp.transition = discontinuous)) = 1)) OR ((closed_curve) AND
(SIZEOF(QUERY(temp <* segments | temp.transition = discontinuous)) = 0));
END_ENTITY;
(*
Attribute definitions:
segments: the component bounded curves, their transitions and senses. The transition attribute for the last segment defines the transition between the end of the last segment and the start of the first; this transition attribute may take the value discontinuous, which indicates an open curve.
self_intersect: indication of whether the curve intersects itself or not; this is for information only;
n_segments: the number of component curves;
closed_curve: indication of whether the curve is closed or not; this is derived from the transition code on the last segment;
Formal propositions:
WR1: No transition code shall be discontinuous, except for the last code of an open curve.

A composite_curve_segment is a type of composite_curve, and is a bounded curve together with transition information which is used to construct a composite_curve.
EXPRESS specification:
*)
ENTITY composite_curve_segment
SUBTYPE OF (founded_item);
transition : transition_code;
same_sense : BOOLEAN;
parent_curve : curve;
INVERSE
using_curves : BAG[1:?] OF composite_curve FOR segments;
WHERE
WR1: ('GEOMETRY_SCHEMA.BOUNDED_CURVE' IN TYPEOF(parent_curve));
END_ENTITY;
(*
Attribute definitions:
transition: the state of transition (i.e., geometric continuity from the last point of this segment to the first point of the next segment) in a composite curve;
same_sense: an indicator of whether or not the sense of the segment agrees with, or opposes, that of the parent curve. If same_sense is false, the point with highest parameter value is taken as the first point of the segment;
parent_curve: the bounded curve which defines the geometry of the segment;
NOTE Since composite_curve_segment is not a subtype of geometric_representation_item the instance of bounded_curve used as parent_curve is not automatically associated with the geometric_representation_context of the representation using a composite_curve containing this composite_curve_segment. It is therefore necessary to ensure that the bounded_curve instance is explicitly included in a representation with the appropriate geometric_representation_context.
using_curves: the set of composite_curves which use this composite_curve_segment as a segment. This set shall not be empty. item supertype.
Formal propositions:
WR1: The parent_curve shall be a bounded_curve.

A reparametrised_composite_curve_segment is a type of composite_curve_segment, which provides the capability to re-define its parametric length without changing its geometry.
Let l = param_length.
If t0 ≤ t ≤ t1 is the parameter range of parent_curve, the new parameter τ for the reparametrised_composite_curve_segment is given by the equation:
τ =(t - t0)l/(t1 - t0), if same_sense = TRUE;
or by the equation:
τ= (t1 - t)l/(t1 - t0), if same_sense = FALSE.
EXPRESS specification:
*)
ENTITY reparametrised_composite_curve_segment
SUBTYPE OF (composite_curve_segment);
param_length : parameter_value;
WHERE
WR1: param_length > 0.0;
END_ENTITY;
(*
Attribute definitions:
param_length: the new parametric length of the segment. The segment is given a simple linear reparametrisation from 0.0 at the first point to param_length at the last point. The parametrisation of the composite curve constructed using this segment is defined in terms of param_length.
Formal propositions:
WR1: The param_length shall be greater than zero.

A pcurve is a type of curve, that is a 3D curve defined by means of a 2D curve in the parameter space of a surface. If the curve is parametrised by the function (u,v) = f(t), and the surface is parametrised by the function (x,y,z) = g(u,v), the pcurve is parametrised by the function (x,y,z) = g(f(t)).
A pcurve definition contains a reference to its basis_surface and an indirect reference to a 2D curve through a definitional_representation entity. The 2D curve, being in parameter space, is not in the context of the basis surface. Thus a direct reference is not possible. For the 2D curve the variables involved are u and v, which occur in the parametric representation of the basis_surface rather than x,y Cartesian coordinates. The curve is only defined within the parametric range of the surface.
EXPRESS specification:
*)
ENTITY pcurve
SUBTYPE OF (curve);
basis_surface : surface;
reference_to_curve : definitional_representation;
WHERE
WR1: SIZEOF(reference_to_curve\representation.items) = 1;
WR2: 'GEOMETRY_SCHEMA.CURVE' IN TYPEOF (reference_to_curve\representation.items[1]);
WR3: reference_to_curve\representation.items[1]\ geometric_representation_item.dim =2;
END_ENTITY;
(*
Attribute definitions:
basis_surface: the surface in whose parameter space the curve is defined;
reference_to_curve: the reference to the parameter space curve which defines the pcurve ;
Formal propositions:
WR1: The set of items in the definitional_representation entity corresponding to the reference_to_curve shall have exactly one element.
WR2: The unique item in the set shall be a curve.
WR3: The dimensionality of this parameter space curve shall be 2.

A bounded_pcurve is a type of pcurve, which also has the properties of a bounded_curve.
EXPRESS specification:
*)
ENTITY bounded_pcurve
SUBTYPE OF (pcurve, bounded_curve);
WHERE
WR1: ('GEOMETRY_SCHEMA.BOUNDED_CURVE' IN TYPEOF(SELF\pcurve.reference_to_curve.items[1]));
END_ENTITY;
(*
Formal propositions:
WR1: The referenced curve of the pcurve supertype shall be of type bounded_curve. This ensures that the bounded_pcurve is of finite arc length.

A surface_curve is a type of curve, that is a curve on a surface. The curve is represented as a curve (curve_3d) in three-dimensional space and possibly as a curve, corresponding to a pcurve, in the two-dimensional parametric space of a surface. The ability of this curve to reference a list of 1 or 2 pcurve_or_surfaces enables this entity to define either a curve on a single surface, or an intersection curve which has two distinct surface associations. A `seam' on a closed surface can also be represented by this entity; in this case each associated_geometry will be a pcurve lying on the same surface. Each pcurve, if it exists, shall be parametrised to have the same sense as curve_3d. The surface_curve takes its parametrisation directly from either curve_3d or pcurve as indicated by the attribute master representation.
NOTE 1 Because of the ANDOR relationship with the bounded_surface_curve subtype an instance of a surface_curve may be any one of the following:
EXPRESS specification:
*)
ENTITY surface_curve
SUPERTYPE OF (ONEOF (intersection_curve,
seam_curve)
ANDOR bounded_surface_curve)
SUBTYPE OF (curve);
curve_3d : curve;
associated_geometry : LIST[1:2] OF pcurve_or_surface;
master_representation : preferred_surface_curve_representation;
DERIVE
basis_surface : SET[1:2] OF surface := get_basis_surface(SELF);
WHERE
WR1: curve_3d.dim = 3;
WR2: ('GEOMETRY_SCHEMA.PCURVE' IN TYPEOF(associated_geometry[1])) OR (master_representation <> pcurve_s1);
WR3: ('GEOMETRY_SCHEMA.PCURVE' IN TYPEOF(associated_geometry[2])) OR (master_representation <> pcurve_s2);
WR4: NOT ('GEOMETRY_SCHEMA.PCURVE' IN TYPEOF(curve_3d));
END_ENTITY;
(*
Attribute definitions:
curve_3d: the curve which is the three-dimensional representation of the surface_curve;
associated_geometry: a list of one or two pcurves or surfaces which define the surface or surfaces associated with the surface curve. Two elements in this list indicate that the curve has two surface associations which need not be two distinct surfaces. When a pcurve is selected, it identifies a surface and also associates a basis curve in the parameter space of this surface;
master_representation: the master_representation defines the curve used to determine the unique parametrisation of the surface_curve.
The master_representation takes one of the values curve_3d, pcurve_s1 or pcurve_s2 to indicate a preference for the 3D curve, or the first or second pcurve, in the associated geometry list, respectively. Multiple representations provide the ability to communicate data in more than one form, even though the data is expected to be geometrically identical.
NOTE 2 The master_representation attribute acknowledges the impracticality of ensuring that multiple forms are indeed identical and allows the indication of a preferred form. This would probably be determined by the creator of the data. All characteristics, such as parametrisation, domain, and results of evaluation, for an entity having multiple representations, are derived from the master representation. Any use of the other representations is a compromise for practical considerations.
basis_surface: the surface, or surfaces on which the surface_curve lies. This is determined from the associated_geometry list.
Formal propositions:
WR1: The currve curve_3d shall be defined in three-dimensional space.
WR2: The value pcurve_s1 shall only be nominated as the master representation if the first element of the associated geometry list is a pcurve.
WR3: The value pcurve_s2 shall only be nominated as the master representation if the second element of the associated geometry list is a pcurve. This also requires that pcurve_s2 shall not be nominated when the associated geometry list contains a single element.
WR4: The curve curve_3d shall not be a pcurve.
Informal propositions:
IP1: Where curve_3d and one or more pcurves exist they shall represent the same mathematical point set. (i.e., They shall coincide geometrically but may differ in parametrisation.)
IP2: curve_3d and any associated pcurves shall agree with respect to their senses.

A intersection_curve is a type of surface_curve, which results from the intersection of two surfaces. It is represented as a special subtype of the surface_curve entity having two distinct surface associations defined via the associated geometry list.
EXPRESS specification:
*)
ENTITY intersection_curve
SUBTYPE OF (surface_curve);
WHERE
WR1: SIZEOF(SELF\surface_curve.associated_geometry) = 2;
WR2: associated_surface(SELF\surface_curve.associated_geometry[1]) <> associated_surface(SELF\surface_curve.associated_geometry[2]);
END_ENTITY;
(*
Formal propositions:
WR1: The intersection curve shall have precisely two associated geometry elements.
WR2: The two associated geometry elements shall be related to distinct surfaces. These are the surfaces which define the intersection curve.

A seam_curve is a type of surface_curve, that is a curve on a closed parametric surface which has two distinct representations as constant parameter curves at the two extremes of the parameter range for the surface.
EXAMPLE The `seam' on a cylinder has representations as the lines u = 0 or u = 360 degrees in parameter space.
EXPRESS specification:
*)
ENTITY seam_curve
SUBTYPE OF (surface_curve);
WHERE
WR1: SIZEOF(SELF\surface_curve.associated_geometry) = 2;
WR2: associated_surface(SELF\surface_curve.associated_geometry[1]) = associated_surface(SELF\surface_curve.associated_geometry[2]);
WR3: 'GEOMETRY_SCHEMA.PCURVE' IN TYPEOF(SELF\surface_curve.associated_geometry[1]);
WR4: 'GEOMETRY_SCHEMA.PCURVE' IN TYPEOF(SELF\surface_curve.associated_geometry[2]);
END_ENTITY;
(*
Formal propositions:
WR1: The seam curve shall have precisely two associated_geometrys.
WR2: The two associated_geometrys shall be related to the same surface.
WR3: The first associated_geometry shall be a pcurve.
WR4: The second associated_geometry shall be a pcurve.

A bounded_surface_curve is a type of surface_curve, which also has the properties of a bounded_curve.
EXPRESS specification:
*)
ENTITY bounded_surface_curve
SUBTYPE OF (surface_curve, bounded_curve);
WHERE
WR1: ('GEOMETRY_SCHEMA.BOUNDED_CURVE' IN TYPEOF(SELF\surface_curve.curve_3d));
END_ENTITY;
(*
Formal propositions:
WR1: The curve_3d attribute of the surface_curve supertype shall be a bounded_curve.

A composite_curve_on_surface is a type of composite_curve, that is a collection of segments which are curves on a surface. Each segment shall lie on the basis surface, and shall reference a bounded_surface_curve, or a bounded_pcurve, or a composite_curve_on_surface.
NOTE A composite_curve_on_surface can be included as the parent_curve attribute of a composite_curve_segment since it is a bounded curve subtype.
There shall be at least positional continuity between adjacent segments. The parametrisation of the composite curve is obtained from the accumulation of the parametric ranges of the segments. The first segment is parametrised from 0 to l1 , and, for i ≥ 2, the i th segment is parametrised from
Σk=1 i-1 lk to Σi k=1 lk ,
where lk is the parametric length (i.e., difference between maximum and minimum parameter values) of the k^th curve segment.
EXPRESS specification:
*)
ENTITY composite_curve_on_surface
SUPERTYPE OF (boundary_curve)
SUBTYPE OF (composite_curve);
DERIVE
basis_surface : SET[0:2] OF surface := get_basis_surface(SELF);
WHERE
WR1: SIZEOF(basis_surface) > 0;
WR2: constraints_composite_curve_on_surface(SELF);
END_ENTITY;
(*
Attribute definitions:
basis_surface: the surface on which the composite curve is defined.;
Formal propositions:
WR1: The basis_surface SET shall contain at least one surface. This ensures that all segments reference curves on the same surface.
WR2: Each segment shall reference a pcurve, or a surface_curve, or a composite_curve_on_surface.
Informal propositions:
IP1: Each parent_curve referenced by a composite_curve_on_surface segment shall be a curve on surface and a bounded curve.

A offset_curve_2d is a type of curve, at a constant distance from a basis curve in two-dimensional space. This entity defines a simple plane-offset curve by offsetting by distance along the normal to basis_curve in the plane of basis_curve.
The underlying curve shall have a well-defined tangent direction at every point. In the case of a composite curve, the transition code between each segment shall be cont_same_gradient or cont_same_gradient_same_curvature.
NOTE The offset_curve_2d may differ in nature from the basis_curve; the offset of a non self-intersecting curve can be self-intersecting. Care should be taken to ensure that the offset to a continuous curve does not become discontinuous.
The offset_curve_2d takes its parametrisation from the basis_curve. The offset_curve_2d is parametrised as
λ(u) = C(u) + d(orthogonal_complement(t)),
where t is the unit tangent vector to the basis curve C(u) at parameter value u, and d is distance.
The underlying curve shall be two-dimensional.,
EXPRESS specification:
*)
ENTITY offset_curve_2d
SUBTYPE OF (curve);
basis_curve : curve;
distance : length_measure;
self_intersect : LOGICAL;
WHERE
WR1: basis_curve.dim = 2;
END_ENTITY;
(*
Attribute definitions:
basis_curve: the curve that is being offset;
distance: the distance of the offset curve from the basis curve. distance may be positive, negative or zero. A positive value of distance defines an offset in the direction which is normal to the curve in the sense of an anti-clockwise rotation through 90 degrees from the tangent vector T at the given point. (This is in the direction of orthogonal_complement(T).)
self_intersect: an indication of whether the offset curve self-intersects; this is for information only.
Formal propositions:
WR1: The The underlying basis_curve shall be defined in two-dimensional space..

A offset_curve_3d is a type of curve, at a constant distance from a basis curve in three-dimensional space. The underlying curve shall have a well-defined tangent direction at every point. In the case of a composite curve the transition code between each segment shall be cont_same_gradient or cont_same_gradient_same_curvature. The offset curve at any point (parameter) on the basis curve is in the direction < v × t > where v is the fixed reference direction and t is the unit tangent to the basis_curve. For the offset direction to be well defined, t shall not at any point of the curve be in the same, or opposite, direction as v .
NOTE The offset_curve_3d may differ in nature from the basis_curve; the offset of a non-self-intersecting curve can be self-intersecting. Care should be taken to ensure that the offset to a continuous curve does not become discontinuous.
The offset_curve_3d takes its parametrisation from the basis_curve. The offset_curve_3d is parametrised as
λ(u) = C(u) + d < v × t > ),
where t is the unit tangent vector to the basis curve C(u) at parameter value u, and d is distance.
EXPRESS specification:
*)
ENTITY offset_curve_3d
SUBTYPE OF (curve);
basis_curve : curve;
distance : length_measure;
self_intersect : LOGICAL;
ref_direction : direction;
WHERE
WR1: (basis_curve.dim = 3) AND (ref_direction.dim = 3);
END_ENTITY;
(*
Attribute definitions:
basis_curve: the curve that is being offset;
distance: the distance of the offset curve from the basis curve; distance may be positive, negative or zero;
self_intersect: an indication of whether the offset curve self-intersects; this is for information only;
ref_direction: the direction used to define the direction of the offset_curve_3d from the basis_curve.
Formal propositions:
WR1: Both the underlying curve and the reference direction shall be in three-dimensional space.
Informal propositions:
IP1: At no point on the curve shall ref_direction be parallel, or opposite to, the direction of the tangent vector.

A curve_replica is a type of curve, and is a replica of a curve in a different location. It is defined by referencing the parent curve and a transformation. The geometric form of the curve produced will be the same as the parent curve, but, where the transformation includes scaling, the dimensions will differ. The curve replica takes its parametric range and parametrisation directly from the parent curve. Where the parent curve is a curve on surface, the replica will not in general share the property of lying on the surface.
EXPRESS specification:
*)
ENTITY curve_replica
SUBTYPE OF (curve);
parent_curve : curve;
transformation : cartesian_transformation_operator;
WHERE
WR1: transformation.dim = parent_curve.dim;
WR2: acyclic_curve_replica (SELF, parent_curve);
END_ENTITY;
(*
Attribute definitions:
parent_curve: the curve that is being copied;
transformation: the cartesian_transformation_operator which defines the location of the curve replica. This transformation may include scaling.
Formal propositions:
WR1: The coordinate space dimensionality of the transformation attribute shall be the same as that of the parent_curve.
WR2: A curve_replica shall not participate in its own definition.

A surface is a type of geometric_representation_item, that can be envisioned as a set of connected points in 3-dimensional space which is always locally 2-dimensional, but need not be a manifold. A surface shall not be a single point or in part, or entirely, a curve.
Each surface has a parametric representation of the formσ(u,v),
where u and v are independent dimensionless parameters. The unit normal N, at any point on the surface, is given by the equation
N (u,v) = < ∂σ/∂ u × ∂ σ /∂ u >
EXPRESS specification:
*)
ENTITY surface
SUPERTYPE OF (ONEOF (elementary_surface,
swept_surface,
bounded_surface,
offset_surface,
surface_replica))
SUBTYPE OF (geometric_representation_item);
END_ENTITY;
(*
Informal propositions:
IP1: A surface has non-zero area.
IP2: A surface is arcwise connected.

A elementary_surface is a type of surface, that is a simple analytic surface with defined parametric representation.
EXPRESS specification:
*)
ENTITY elementary_surface
SUPERTYPE OF (ONEOF (plane,
cylindrical_surface,
conical_surface,
spherical_surface,
toroidal_surface))
SUBTYPE OF (surface);
position : axis2_placement_3d;
END_ENTITY;
(*
Attribute definitions:
position: the location and orientation of the surface,this attribute is used in the definition of the parametrisation of the surface.

A plane is a type of elementary_surface, that is an unbounded surface with a constant normal. A plane is defined by a point on the plane and the normal direction to the plane.
The data is to be interpreted as follows:
C = position.location
x = position.p[1]
y = position.p[2]
z = position.p[3] (normal to plane)
and the surface is parametrised as
σ(u,v) = C + u x + v y
where the parametrisation range is -∞ < u, v < ∞.
In the above parametrisation, the length unit for the unit vectors x and y is derived from the context of the plane.
EXPRESS specification:
*)
ENTITY plane
SUBTYPE OF (elementary_surface);
END_ENTITY;
(*

A cylindrical_surface is a type of elementary_surface, that is a surface at a constant distance (the radius)from a straight line. A cylindrical_surface is defined by its radius and its orientation and location.
The data is to be interpreted as follows:
C = position.location
x = position.p[1]
y = position.p[2]
z = position.p[3] (axis of cylindrical_surface)
R = radius
and the surface is parametrised as
σ(u,v) = C + R((cos u)x + (sin u)y) + v z
where the parametrisation range is 0 ≤ u ≤ 360 degrees and -∞ < v < ∞. In the above parametrisation the length unit for the unit vector z is equal to that of the radius. u is an angular parameter and when a numerical value is specified it shall use the current units for plane_angle_measure.
In the placement coordinate system defined above, the surface is represented by the equation S = 0, where
S(x, y, z) = x2 + y2 - R2
The positive direction of the normal to the surface at any point on the surface is given by:
( Sx, Sy, Sz ).
The unit normal is given by
N (u,v) = (cos(u))x + (sin (u))y.
The sense of this normal is away from the axis of the cylinder.
EXPRESS specification:
*)
ENTITY cylindrical_surface
SUBTYPE OF (elementary_surface);
radius : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
radius: the radius of the cylinder.

A conical_surface is a type of elementary_surface, which could be produced by revolving a line in 3-dimensional space about any intersecting line. A conical_surface is defined by the semi-angle, the location and orientation and by the radius of the cone in the plane passing through the location point C normal to the cone axis.
NOTE 1 This form of representation is designed to provide the greatest geometric precision for those parts of the surface which are close to the location point C. For this reason the apex should only be selected as location point if the region of the surface close to the apex is of interest.
The data is to be interpreted as follows:
C = position.location
x = position.p[1]
y = position.p[2]
z = position.p[3] (axis of conical_surface)
R = radius
α = radius
and the surface is parametrised as
σ(u,v) = C + (R + v tan α)((cos u) x + (sin u)y) + vz
where the parametrisation range is 0 ≤ u ≤ 360 degrees and -∞ < v < ∞. In the above parametrisation the length unit for the unit vector z is equal to that of the radius. u is an angular parameter and when a numerical value is specified it shall use the current units for plane_angle_measure. In the placement coordinate system defined above, the surface is represented by the equation S = 0, whereS(x, y, z) = x2 + y2 - (R + ztan α)2
The positive direction of the normal to the surface at any point on the surface is given by
( Sx, Sy, Sz ).
The unit normal is given by
N (u,v) = ((cos u)x + (sin u)y - (tan α)z)/( (√(1 + (tan α)2)), if R + v tan α > 0.0
N(u,v) = - ((cos u)x + (\sin u)y - (tan α)z)/ (√(1 + (tan α)2)), if R + v tan α < 0.0.
NOTE 2 The normal to the surface is undefined at the point where R + v tan α = 0.0.
The sense of the normal is away from the axis of the cone. If the radius is zero, the cone apex is at the point (0, 0, 0) in the placement coordinate system (i.e., at SELF\elementary_surface.position.location).
EXPRESS specification:
*)
ENTITY conical_surface
SUBTYPE OF (elementary_surface);
radius : length_measure;
semi_angle : plane_angle_measure;
WHERE
WR1: radius >= 0.0;
END_ENTITY;
(*
Attribute definitions:
radius: the radius of the circular curve of intersection between the cone and a plane perpendicular to the axis of the cone passing through the location point (i.e., SELF\elementary_surface.position.location);
semi_angle: the cone semi-angle.
NOTE 3 See Figure (14) 14 for illustration of the attributes.
Formal propositions:
WR1: The radius shall not be negative.

A spherical_surface is a type of elementary_surface, which is at a constant distance (the radius) from a central point. A spherical_surface is defined by the radius and the location and orientation of the surface.
The data is to be interpreted as follows:
C = position.location
x = position.p[1]
y = position.p[2]
z = position.p[3] (axis of spherical_surface)
R = radius
and the surface is parametrised as
σ(u,v) = C + R cos v ((cos u) x + (sin u) y) + R(sin v) z
where the parametrisation range is 0 ≤ u ≤ 360 degrees and -90 ≤ v ≤ 90 degrees.
u and v are angular parameters and when numerical values are specified they shall use the current units for plane_angle_measure.
In the placement coordinate system defined above, the surface is represented by the equation S = 0, whereS(x, y, z) = x2 + y2 + z2 - R2.
The positive direction of the normal to the surface at any point on the surface is given by
( Sx, Sy, Sz ).
The unit normal is given by
N (u,v) = cos v((cos u)x + (sin u)y) + (sin v)z,
EXPRESS specification:
*)
ENTITY spherical_surface
SUBTYPE OF (elementary_surface);
radius : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
radius: the radius of the sphere.

A toroidal_surface is a type of elementary_surface, which could be produced by revolving a circle about a line in its plane. The radius of the circle being revolved is referred to here as the minor_radius and the major_radius is the distance from the centre of this circle to the axis of revolution. A toroidal_surface is defined by the major and minor radii and the position and orientation of the surface.
The data is to be interpreted as follows:
C = position.location
x = position.p[1]
y = position.p[2]
z = position.p[3] (axis of toroidal_surface)
R = major_radius
r = minor_radius
and the surface is parametrised as
σ(u,v) = C + (R + rcos v)((cosu)x + (sin u))y) + r(sinv))z
where the parametrisation range is 0 ≤ u, v ≤ 360 degrees.
u and v are angular parameters and when numerical values are specified they shall use the current units for plane_angle_measure.
In the placement coordinate system defined above, the surface is represented by the equation S = 0, where
S(x, y, z) = x2 + y2 + z2 -2R√(x2+y2) - r2 + R2.
The positive direction of the normal to the surface at any point on the surface is given by
( Sx, Sy, Sz ).
The unit normal is given by
N (u,v) = cosv((cos u)x + (sin u)y) + (sin v)z.
The sense of this normal is away from the nearest point on the circle of radius R with centre C. A manifold surface will be produced if the major radius is greater than the minor radius. If this condition is not fulfilled, the resulting surface will be self-intersecting.
EXPRESS specification:
*)
ENTITY toroidal_surface
SUBTYPE OF (elementary_surface);
major_radius : positive_length_measure;
minor_radius : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
major_radius: the major-radius of the torus;
minor_radius: the minor-radius of the torus.

A degenerate_toroidal_surface is a type of toroidal_surface, in which the minor_radius is greater than the major_radius. In this subtype the parametric range is restricted in order to define a manifold surface which is either the inner 'lemon-shaped' surface, or the outer 'apple-shaped' portion of the self-intersecting surface defined by the supertype.
The data is to be interpreted as follows:
C = position.location
x = position.p[1]
y = position.p[2]
z = position.p[3] (axis of degenerate_toroidal_surface)
R = major_radius
r = minor_radius
and the surface is parametrised as
σ(u,v) = C + (R + rcos v)((cosu)x + (sin u))y) + r(sinv))z
where the parametrisation range is
If select_outer = .TRUE. :
0 ≤ u ≤ 360 degrees. -φ ≤ v ≤ φ degrees.
If select_outer = .FALSE. :
0 ≤ u ≤ 360 degrees. φ ≤ v ≤ 360 - φ degrees.
Where φ degrees is the angle given by rcos φ = -R . u and v are angular parameters and when numerical values are specified they shall use the current units for plane_angle_measure.
NOTE 1 When select_outer = .FALSE. the surface normal points out of the enclosed volume and is defined by the equation
N (u,v) = cos v((cos u)x + (sinu)y) + (sin v)z.
The sense of this normal is away from the furthest point on the circle of radius R in the plane normal to z centred at C.
The sense of this normal is opposite to the direction of
(∂ σ)/(∂ u) × (∂ σ)/(∂ v) .
NOTE 2 See Figure (15) for illustration of the attributes.
EXPRESS specification:
*)
ENTITY degenerate_toroidal_surface
SUBTYPE OF (toroidal_surface);
select_outer : BOOLEAN;
WHERE
WR1: major_radius < minor_radius;
END_ENTITY;
(*
Attribute definitions:
select_outer: a BOOLEAN flag used to distinguish between the two portions of the degenerate_toroidal_surface. If select_outer is true, the outer portion of the surface is selected and a closed `apple-shaped' axi-symmetric surface is defined. If select_outer is false, the inner portion is selected to define a closed 'lemon-shaped' axi-symmetric surface.
Formal propositions:
WR1: The major radius shall be less than the minor radius.

A dupin_cyclide_surface is a type of elementary_surface, that is a generalisation of a toroidal_surface in which the radius of the generatrix varies as it is swept around the directrix, passing through a maximum and a minimum value. The directrix is in general an ellipse, though that fact is not germane to the definition given here. The surface has two orthogonal planes of symmetry, and in both of them its cross-section is a pair of circles.
NOTE 1 These circles are illustrated in Figure 15, where the upper cross-section contains the generatrix circles of maximum and minimum radius, and the lower cross-section is in the plane of the directrix.
NOTE 2 Further details of the properties and applications of this useful but unfamiliar surface may be found in PRATT [13],[14], and the further references they contain.
As with the toroidal_surface, self-intersecting forms occur. The Dupin cyclides are special cases of a more general class of surfaces known as generalized cyclides (or sometimes simply cyclides). The present specification does not cover the wider class.
The interpretation of the data is as follows:
C = position.location
x = position.p[1]
y = position.p[2]
z = position.p[3] (axis of toroidal_surface)
R = generalised_major_radius
r = generalised_minor_radius
s = skewness
and the surface is parametrised as

where the domain of parametrisation is 0° ≤ u,v ≤ 360° , and √ denotes the positive square root. u and v are angular parameters and when numerical values are specified they shall use the current units for plane_angle_measure.
NOTE 3 The three parameters r,R and s determine the centres and radii of the circles in the planes of symmetry, as shown in Figure 15. Conversely, knowledge of the geometry of these circles allows the defining cyclide parameters to be determined. In the upper and lower diagrams respectively of Figure 15 the circles have parameter values u = 0° (right), u = 180° (left), v = 0° (inner) and v = 180° (outer). The point with parameter values (0,0) is the extreme point on the positive x-axis. The parameter u runs anticlockwise around both circles in the lower diagram, and the parameter v runs clockwise round the left-hand circle and anticlockwise round the right-hand circle in the upper diagram.
In the placement coordinate system defined above the Dupin cyclide surface has the algebraic representation S = 0, where
S = (x2 + y2 + z2 + R2 - r2 - s2)2 - 4(Rx - rs)2- 4(R2 - s2)y2.
The positive direction of the normal vector at any point on the surface is given by
(Sx,Sy,Sz).
In parametric terms, the unit surface normal vector is
N (u,v) = (R \cos ucosv + s)x + (√(R2 - s2)sinucosv)y + (√(R2 - s2)sinv)z
This enables the parametric surface representation to be rewritten as
σ(u,v) = σ 0(u,v) + r N (u,v),
which shows that any Dupin cyclide with given values of R and s is a parallel offset from a base Dupin cyclide σ 0(u,v) with the same values of R,s but with r = 0.
Further, the offset distance is precisely r. This generalizes an important property of the torus.
The Dupin cyclide is a manifold surface under the conditions 0 ≤ s < r < R. This form is known as a ring cyclide. Self-intersecting forms arise when the circles in either plane of symmetry intersect. The conditions 0 < r ≤ s < R give a horned cyclide and the conditions 0 ≤ s ≤ R < r a spindle cyclide. The sense of the surface normal given above is outwards from both circles in the upper view and from the annular region in the lower cross-sectional view in Figure 15. For the ring cyclide this means that it is outwards-pointing over the entire surface. For the horned cyclide the normal is inward-pointing over the smaller portion of the surface lying between the two self-intersection points. For the spindle cyclide the `spindle' corresponds to the `lemon' solid arising in the case of a self-intersecting torus. For this case of the Dupin cyclide the normal is outward-pointing over both the `apple' and 'lemon' solids enclosed by the surface.
NOTE 4 The three forms of the Dupin cyclide are shown in Figures 16, 17, 18 and 19. In Figure 18 part of the exterior surface is removed to reveal the inner surface.
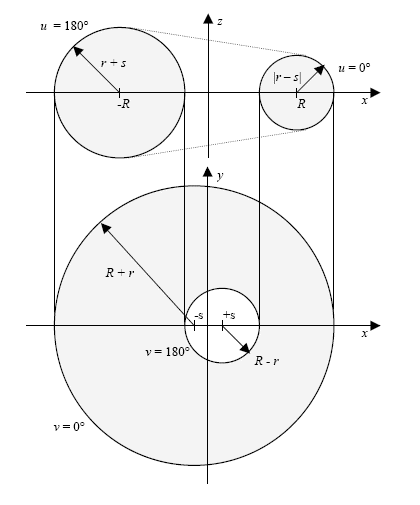

NOTE 5 For ISO 10303 purposes, the values of R and r are of type positive_length_measure and s is non-negative. The surface defined by the foregoing equations when one or more of R, r and s is negative corresponds to a reparametrisation of a Dupin cyclide for which these constants are all non-negative.
NOTE 6 Both families of isoparametric curves of the Dupin cyclide consist of circles.
NOTE 7 Dupin cyclides can be used to construct smooth joins between cylindrical and/or conical surfaces whose (possibly skew) axes have arbitrary relative orientations. Additionally, smooth T-junctions between cones and cylinders can be designed using Dupin cyclides.
NOTE 8 Dupin cyclides also have uses as blending surfaces in solid modeling, generalising the use of the torus for this purpose.
NOTE 9 The Dupin cyclide as defined here is a quartic (degree four) algebraic surface of bounded extent. There also exists a cubic Dupin cyclide of infinite extent, not currently defined in this part of ISO 10303.
EXPRESS specification:
*)
ENTITY dupin_cyclide_surface
SUBTYPE OF (elementary_surface);
generalised_major_radius : positive_length_measure;
generalised_minor_radius : positive_length_measure;
skewness : length_measure;
WHERE
WR1: skewness >= 0.0;
END_ENTITY;
(*
Attribute definitions:
generalised_major_radius: the mean of the radii of the two circles forming the cyclide cross-section in the plane of the directrix;
generalised_minor_radius: the mean of the radii of the largest and smallest generatrix circles;
skewness: half the difference between the radii of the two cross-sectional circles in either plane of symmetry; when the skewness attribute is zero the surface is a torus; otherwise, its value determines the degree of asymmetry of the surface about the third plane perpendicular to its two planes of symmetry.
Formal propositions:
WR1: The skewness shall not be negative.

A swept_surface is a type of surface, that is constructed by sweeping a curve along another curve.
EXPRESS specification:
*)
ENTITY swept_surface
SUPERTYPE OF (ONEOF (surface_of_linear_extrusion,
surface_of_revolution,
surface_curve_swept_surface,
fixed_reference_swept_surface))
SUBTYPE OF (surface);
swept_curve : curve;
END_ENTITY;
(*
Attribute definitions:
swept_curve: the curve to be swept in defining the surface; if the swept curve is a pcurve, it is the image of this curve in 3D geometric space which is swept, not the parameter space curve.

A surface_of_linear_extrusion is a type of swept_surface, or a generalised cylinder obtained by sweeping a curve in a given direction.
The parametrisation is as follows, where the curve has a parametrisation λ(u), and V = extrusion_axis
σ(u,v) = λ(u) + v V
The parametrisation range for v is -∞ < v < ∞ and for u is defined by the curve parametrisation.
EXPRESS specification:
*)
ENTITY surface_of_linear_extrusion
SUBTYPE OF (swept_surface);
extrusion_axis : vector;
END_ENTITY;
(*
Attribute definitions:
extrusion_axis: the direction of extrusion, the magnitude of this vector determines the parametrisation;
Informal propositions:
IP1: The surface shall not self-intersect.

A surface_of_revolution is a type of swept_surface, obtained by rotating a curve one complete revolution about an axis.
The data shall be interpreted as below.
The parametrisation is as follows, where the curve has a parametrisation λ(v), C = position.location and V = position.z
σ(u,v) = C + (λ (v) - C)cosu + ((λ(v) - C)⋅ V)V(1 - cosu) + V× ( λ(v) - C)sinu
In order to produce a single-valued surface with a complete revolution, the curve shall be such that when expressed in a cylindrical coordinate system (r,φ,z) centred at C with axis V, no two distinct parametric points on the curve shall have the same values for (r,z).
NOTE 1 In this context a single valued surface is interpreted as one for which the mapping, from the interior of the rectangle in parameter space corresponding to its parametric range, to geometric space, defined by the surface equation, is one-to-one.
For a surface of revolution the parametric range is 0 ≤ u ≤ 360 degrees. u is an angular parameter and when a numerical value is specified it shall use the current units for plane_angle_measure.
The parameter range for v is defined by the referenced curve.NOTE 2 The geometric shape of the surface is not dependent upon the curve parametrisation.
EXPRESS specification:
*)
ENTITY surface_of_revolution
SUBTYPE OF (swept_surface);
axis_position : axis1_placement;
DERIVE
axis_line : line := representation_item('')|| geometric_representation_item()|| curve()|| line(axis_position.location, representation_item('')||
geometric_representation_item()|| vector(axis_position.z, 1.0));
END_ENTITY;
(*
Attribute definitions:
axis_position: a point on the axis of revolution and the direction of the axis of revolution;
axis_line: the line coinciding with the axis of revolution.
Informal propositions:
IP1: The surface shall not self-intersect.
IP2: The swept_curve shall not be coincident with the axis_line for any finite part of its length.

A surface_curve_swept_surface is a type of swept_surface, which is the result of sweeping a curve along a directrix curve lying on the reference_surface. The orientation of the swept_curve during the sweeping operation is related to the normal to the reference_surface.
The swept_curve is required to be a curve lying in the plane z = 0 and this is swept along the directrix in such a way that the origin of the local coordinate system used to define the swept_curve is on the directrix and the local X axis is in the direction of the normal to the reference_surface. The resulting surface has the property that the cross section of the surface by the normal plane to the directrix at any point is a copy of the swept_curve.
The orientation of the swept_curve as it sweeps along the directrix is precisely defined by a cartesian_transformation_operator_3d with attributes:
local_origin as point (0,0,0),
axis1 as the normal N to the reference_surface at the point of the directrix with parameter u.
axis3 as the direction of the tangent vector t at the point of the directrix with parameter u.
The remaining attributes are defaulted to define a corresponding transformation matrix T(u).
NOTE 1 In the special case where the directrix is a planar curve the reference_surface is the plane of the directrix and the normal N is a constant.
The parametrisation is as follows, where the directrix has parametrisation μ(u) and the swept_curve curve has a parametrisation λ(v),
μ (u) = Point on directrix,
T (u) = Transformation matrix at parameter (u):
σ(u,v) = μ(u) + T((u))λ (v)
In order to produce a continuous surface the directrix curve shall be tangent continuous.
For a surface_curve_swept_surface the parameter range for u is defined by the directrix curve.
The parameter range for v is defined by the referenced swept_curve.NOTE 2 The geometric shape of the surface is not dependent upon the curve parametrisations.
EXPRESS specification:
*)
ENTITY surface_curve_swept_surface
SUBTYPE OF (swept_surface);
directrix : curve;
reference_surface : surface;
WHERE
WR1: (NOT ('GEOMETRY_SCHEMA.SURFACE_CURVE' IN TYPEOF(directrix))) OR (reference_surface IN (directrix\surface_curve.basis_surface));
END_ENTITY;
(*
Attribute definitions:
directrix: the curve used to define the sweeping operation; the surface is generated by sweeping the swept_curve along the directrix.
reference_surface: the surface containing the directrix.
Formal propositions:
WR1: If the directrix is a surface_curve then the reference_surface shall be in the basis_surface set for this curve.
Informal propositions:
IP1: The swept_curve shall be a curve lying in the plane z = 0.
IP2: The directrix shall be a curve lying on the reference_surface.

A fixed_reference_swept_surface is a type of swept_surface, which is the result of sweeping a curve along a directrix. The orientation of the curve during the sweeping operation is controlled by the fixed_reference direction. The swept_curve is required to be a curve lying in the plane z = 0 and this is swept along the directrix in such a way that the origin of the local coordinate system used to define the swept_curve is on the directrix and the local X axis is in the direction of the projection of fixed_reference onto the normal plane to the directrix at this point. The resulting surface has the property that the cross section of the surface by the normal plane to the directrix at any point is a copy of the swept_curve.
The orientation of the swept_curve as it sweeps along the directrix is precisely defined by a cartesian_transformation_operator_3d with attributes:
local_origin as point (0,0,0),
axis1 as fixed_reference,
axis3 as the direction of the tangent vector t at the point of the directrix with parameter u.
The remaining attributes are defaulted to define a corresponding transformation matrix T (u).
The parametrisation is as follows, where the directrix has parametrisation μ(u) and the swept_curve curve has a parametrisation λ(v),
μ(u) = Point on directrix,
T (u) = Transformation matrix at parameter (u):
σ(u,v) = μ(u) + T (u)λ(v)
In order to produce a continuous surface the directrix curve the curve shall be tangent continuous.
For a fixed_reference_swept_surface the parameter range for u is defined by the directrix curve. The parameter range for v is defined by the referenced swept_curve.NOTE 1 The geometric shape of the surface is not dependent upon the curve parametrisations.
NOTE 2 The attributes are illustrated in Figure (20).
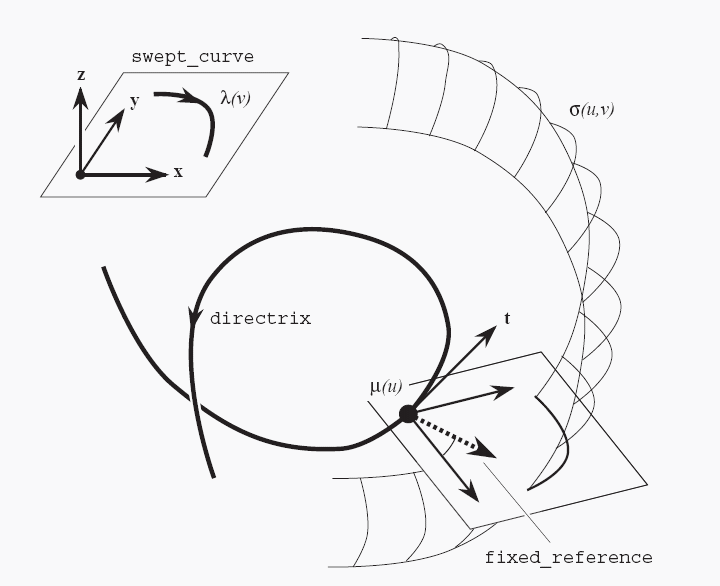
EXPRESS specification:
*)
ENTITY fixed_reference_swept_surface
SUBTYPE OF (swept_surface);
directrix : curve;
fixed_reference : direction;
END_ENTITY;
(*
Attribute definitions:
directrix: the curve used to define the sweeping operation. The surface is generated by sweeping the swept_curve along the directrix.
fixed_reference: the direction used to define the orientation of swept_curve as it sweeps along the directrix..
Informal propositions:
IP1: The swept_curve shall be a curve lying in the plane z = 0.
IP2: The fixed_reference shall not be parallel to a tangent vector to the directrix at any point along this curve.

A bounded_surface is a type of surface of finite area with identifiable boundaries.
EXPRESS specification:
*)
ENTITY bounded_surface
SUPERTYPE OF (ONEOF (b_spline_surface,
rectangular_trimmed_surface,
curve_bounded_surface,
rectangular_composite_surface,
locally_refined_spline_surface))
SUBTYPE OF (surface);
END_ENTITY;
(*
Informal propositions:
IP1: A bounded_surface has a finite non-zero surface area.
IP2: A bounded_surface has boundary curves.

A b_spline_surface is a type of bounded_surface, and is a general form of rational or polynomial parametric surface which is represented by control points, basis functions, and possibly, weights. As with the corresponding curve entity it has some special subtypes where some of the data can be derived.
NOTE 1 Identification of B-spline surface default values and subtypes is important for performance considerations and for efficiency issues in performing computations.
NOTE 2 A B-spline is rational if and only if the weights are not all identical. If it is polynomial, the weights may be defaulted to all being 1.
NOTE 3 In the case where the B-spline surface is uniform, quasi-uniform or piecewise Bézier, the knots and knot multiplicities may be defaulted (i.e., non-existent in the data as specified by the attribute definitions). When the knots are defaulted, a difference of 1.0 between separate knots is assumed, and the effective parameter range for the resulting surface starts from 0.0. These defaults are provided by the subtypes.
NOTE 4 The knots and knot multiplicities shall not be defaulted in the non-uniform case.
NOTE 5 The defaulting of weights and knots are done independently of one another.
The data is to be interpreted as follows:
The symbology used here is:
K1 = upper_index_on_u_control_points
K2 = upper_index_on_v_control_points
P ij = control_points
wij = weights
d1 = u_degree
d1 = u_degree
The control points are ordered as
P 00, P 01, P 02, . . . . P K1(K2-1, P K1K2.
The weights, in the case of the rational subtype, are ordered similarly.
For each parameter, s = u or v, if k is the upper index on the control points and d is the degree for s, the knot array is an array of (k + d + 2) real numbers [s-d, ... ,sk+1], such that for all indices j in [-d, k], sj ≤ sj+1 . This array is obtained from the appropriate u_knots or v_knots list by repeating each multiple knot according to the multiplicity.
Ni d , the ith normalised B-spline basis function of degree d, is defined on the subset [si-d, ... ,si+1] of this array.
Let L denote the number of distinct values amongst the knots in the knot list; L will be referred to as the `upper index on knots'. Let mj denote the multiplicity (i.e., number of repetitions) of the jth distinct knot value. Then:
ΣL i=1 mi = d + k + 2
All knot multiplicities except the first and the last shall be in the range 1, . . . , d; the first and last may have a maximum value of d + 1.NOTE 6 In evaluating the basis functions, a knot u of, for example, multiplicity 3 is interpreted as a sequence u, u, u, in the knot array.
The surface_form is used to identify specific quadric surface types (which shall have degree two), ruled surfaces and surfaces of revolution. As with the b_spline_curve, the surface_form is informational only and the spline data takes precedence.
The surface is to be interpreted as follows:
In the polynomial case the surface is given by the equation:
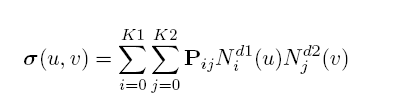
In the rational case the surface equation is:
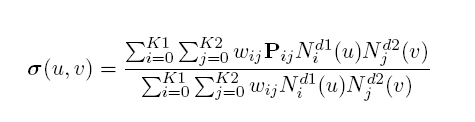
NOTE 7 Definitions of the B-spline basis functions, Ni d1(u) and Ni d2(v), can be found in [1], [5] and [6]. It should be noted that there is a difference in terminology between these references.
EXPRESS specification:
*)
ENTITY b_spline_surface
SUPERTYPE OF (ONEOF (b_spline_surface_with_knots,
uniform_surface,
quasi_uniform_surface,
bezier_surface)
ANDOR rational_b_spline_surface)
SUBTYPE OF (bounded_surface);
u_degree : INTEGER;
v_degree : INTEGER;
control_points_list : LIST[2:?] OF LIST[2:?] OF cartesian_point;
surface_form : b_spline_surface_form;
u_closed : LOGICAL;
v_closed : LOGICAL;
self_intersect : LOGICAL;
DERIVE
u_upper : INTEGER := SIZEOF(control_points_list) - 1;
v_upper : INTEGER := SIZEOF(control_points_list[1]) - 1;
control_points : ARRAY[0:u_upper] OF ARRAY[0:v_upper] OF cartesian_point := make_array_of_array(control_points_list, 0,u_upper,0,v_upper);
WHERE
WR1: ('GEOMETRY_SCHEMA.UNIFORM_SURFACE' IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.QUASI_UNIFORM_SURFACE' IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.BEZIER_SURFACE'
IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.B_SPLINE_SURFACE_WITH_KNOTS' IN TYPEOF(SELF));
END_ENTITY;
(*
Attribute definitions:
u_degree: algebraic degree of basis functions in u;
v_degree: algebraic degree of basis functions in v;
control_points_list: a list of lists of control points;
surface_form: an indicator of special surface types;
u_closed: indication of whether the surface is closed in the u direction; this is for information only;
v_closed: indication of whether the svrface is closed in the v direction; this is for information only;
self_intersect: a flag to indicate whether, or not, surface is self-intersecting; this is for information only.
u_upper: the upper index on control points in u direction;
v_upper: the upper index on control points in v direction;
control_points: an array (two-dimensional) of control points defining surface geometry. This array is constructed from the control points list.
Formal propositions:
WR1: Any instantiation of this entity shall include one of the subtypes
b_spline_surface_with_knots, uniform_surface, quasi_uniform_surface, or bezier_surface.

A b_spline_surface_with_knots is a type of b_spline_surface, in which the knot values are explicitly given. This subtype shall be used to represent non-uniform B-spline surfaces, and may also be used for other knot types. All knot multiplicities except the first and the last shall be in the range 1, . . . , d; the first and last may have a maximum value of d + 1.
NOTE In evaluating the basis functions, a knot u of, for example, multiplicity 3 is interpreted as a sequence u, u, u, in the knot array.
EXPRESS specification:
*)
ENTITY b_spline_surface_with_knots
SUBTYPE OF (b_spline_surface);
u_multiplicities : LIST[2:?] OF INTEGER;
v_multiplicities : LIST[2:?] OF INTEGER;
u_knots : LIST[2:?] OF parameter_value;
v_knots : LIST[2:?] OF parameter_value;
knot_spec : knot_type;
DERIVE
knot_u_upper : INTEGER := SIZEOF(u_knots);
knot_v_upper : INTEGER := SIZEOF(v_knots);
WHERE
WR1: constraints_param_b_spline(SELF\b_spline_surface.u_degree, knot_u_upper, SELF\b_spline_surface.u_upper, u_multiplicities,
u_knots);
WR2: constraints_param_b_spline(SELF\b_spline_surface.v_degree, knot_v_upper, SELF\b_spline_surface.v_upper, v_multiplicities,
v_knots);
WR3: SIZEOF(u_multiplicities) = knot_u_upper;
WR4: SIZEOF(v_multiplicities) = knot_v_upper;
END_ENTITY;
(*
Attribute definitions:
u_multiplicities: the multiplicities of the knots in the u parameter direction;
v_multiplicities: the multiplicities of the knots in the v parameter direction;
u_knots: the list of the distinct knots in the u parameter direction;
v_knots: the list of the distinct knots in the v parameter direction;
knot_spec: the description of the knot type;
knot_u_upper: the number of distinct knots in the u parameter direction;
knot_v_upper: the number of distinct knots in the v parameter direction;
Formal propositions:
WR1: The function constraints_param_b_spline returns TRUE when the parameter constraints are verified for the u direction.
WR2: The function constraints_param_b_spline returns TRUE when the parameter constraints are verified for the v direction.
WR3: The number of u_multiplicities shall be the same as the number of u_knots.
WR4: The number of v_multiplicities shall be the same as the number of v_knots.

A uniform_surface is a type of b_spline_surface, in which the knots are evenly spaced. Suitable default values for the knots and knot multiplicities can be derived in this case. A B-spline is uniform if and only if all knots are of multiplicity and they differ by a positive constant from the preceding knot. In this subtype the knot spacing is 1.0, starting from -degree.
NOTE If explicit knot values for the surface are required, they can be derived as follows:
ku_up = SELF\backslash b_spline_surface.u_upper + SELF\backslash b_spline_surface.u_degree + 2,
kv_up = SELF\backslash b_spline_surface.v_upper + SELF\backslash b_spline_surface.v_degree + 2 .
ku_up is the value required for the upper index on the knot and knot multiplicity lists in the u direction. This is computed from the degree and the number of control points in this direction.
kv_up is the value required for the upper index on the knot and knot multiplicity lists in the v direction. This is computed from the degree and the number of control points in this direction.
The knot multiplicities and knots in the u and v parameter directions are then given by the function calls:
default_b_spline_knot_mult(SELF\b_spline_surface.u_degree, ku_up, uniform_knots)
default_b_spline_knots(SELF\b_spline_surface.u_degree, ku_up, uniform_knots)
default_b_spline_knot_mult(SELF\b_spline_surface.v_degree, kv_up, uniform_knots)
default_b_spline_knots(SELF\b_spline_surface.v_degree, kv_up, uniform_knots)
EXPRESS specification:
*)
ENTITY uniform_surface
SUBTYPE OF (b_spline_surface);
END_ENTITY;
(*

A quasi_uniform_surface is a type of b_spline_surface, in which the knots are evenly spaced, and except for the first and last, have multiplicity 1. Suitable default values for the knots and knot multiplicities are derived in this case. A B-spline is quasi-uniform if and only if the knots are of multiplicity (degree+1) at the ends, of multiplicity 1 elsewhere, and they differ by a positive constant from the preceding knot. In this subtype the knot spacing is 1.0, starting from 0.0.
NOTE If explicit knot values for the surface are required, they can be derived as follows:
ku_up = SELF\backslash b_spline_surface.u_upper - SELF\backslash b_spline_surface.u_degree + 2,
kv_up = SELF\backslash b_spline_surface.v_upper - SELF\backslash b_spline_surface.v_degree + 2.
ku_up is the value required for the upper index on the knot and knot multiplicity lists in the u direction. This is computed from the degree and the number of control points in this direction.
kv_up is the value required for the upper index on the knot and knot multiplicity lists in the v direction. This is computed from the degree and the number of control points in this direction.
The knot multiplicities and knots in the u and v parameter directions are then given by the function calls:
default_b_spline_knot_mult(SELF\b_spline_surface.u_degree, ku_up, quasi_uniform_knots)
default_b_spline_knots(SELF\b_spline_surface.u_degree, ku_up, quasi_uniform_knots)
default_b_spline_knot_mult(SELF\b_spline_surface.v_degree, kv_up, quasi_uniform_knots)
default_b_spline_knots(SELF\b_spline_surface.v_degree, kv_up, quasi_uniform_knots)
EXPRESS specification:
*)
ENTITY quasi_uniform_surface
SUBTYPE OF (b_spline_surface);
END_ENTITY;
(*

A bezier_surface is a type of b_spline_surface, in which the knots are evenly spaced and have high multiplicities. Suitable default values for the knots and knot multiplicities are derived in this case. In this subtype the knot spacing is 1.0, starting from 0.0.
NOTE If explicit knot values for the surface are required, they can be derived as follows:
ku_up = (SELF\backslash b_spline_surface.u_upper)/(SELF\backslash b_spline_surface.u_degree) + 1,
kv_up = (SELF\backslash b_spline_surface.v_upper)/(SELF\backslash b_spline_surface.v_degree) + 1,
ku_up is the value required for the upper index on the knot and knot multiplicity lists in the u direction. This is computed from the degree and the number of control points in this direction.
kv_up is the value required for the upper index on the knot and knot multiplicity lists in the v direction. This is computed from the degree and the number of control points in this direction.
The knot multiplicities and knots in the u and v parameter directions are then given by the function calls:
default_b_spline_knot_mult(SELF\b_spline_surface.u_degree, ku_up, bezier_knots)
default_b_spline_knots(SELF\b_spline_surface.u_degree, ku_up, bezier_knots)
default_b_spline_knot_mult(SELF\b_spline_surface.v_degree, kv_up, bezier_knots)
default_b_spline_knots(SELF\b_spline_surface.v_degree, kv_up, bezier_knots)
EXPRESS specification:
*)
ENTITY bezier_surface
SUBTYPE OF (b_spline_surface);
END_ENTITY;
(*

A rational_b_spline_surface is a type of b_spline_surface, which is a piecewise parametric rational surface described in terms of control points, associated weight values and basis functions. It is instantiated with any of the other subtypes of b_spline_surface, which provide explicit or implicit knot values from which the basis functions are defined.
The surface is to be interpreted as follows:
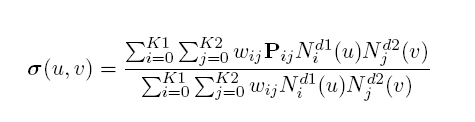
NOTE See b_spline_surface for details of the symbology used in the above equation.
EXPRESS specification:
*)
ENTITY rational_b_spline_surface
SUBTYPE OF (b_spline_surface);
weights_data : LIST[2:?] OF LIST[2:?] OF REAL;
DERIVE
weights : ARRAY[0:u_upper] OF ARRAY[0:v_upper] OF REAL := make_array_of_array(weights_data,0,u_upper,0,v_upper);
WHERE
WR1: (SIZEOF(weights_data) = SIZEOF(SELF\b_spline_surface.control_points_list)) AND (SIZEOF(weights_data[1]) = SIZEOF(SELF\b_spline_surface.control_points_list[1]));
WR2: surface_weights_positive(SELF);
END_ENTITY;
(*
Attribute definitions:
weights_data: the weights associated with the control points in the rational case;
weights: the array (two-dimensional) of weight values constructed from the weights_data.
Formal propositions:
WR1: The array dimensions for the weights shall be consistent with the control points data.
WR2: The weight value associated with each control point shall be greater than zero.

A locally_refined_spline_surface is a type of bounded_surface that is a piecewise parametric polynomial or rational surface described in terms of control points and local B-spline functions. If the set of B-spline functions are linearly independent, they will form a basis. With appropriate attribute values, the surface is capable of representing single span or spline surfaces of explicit polynomial, rational, Bézier or B-spline type. However, the locally_ refined_spline_surface entity is intended for spline surfaces that do not have a tensor product structure. The degree of the surface can vary as the B-splines from which it is defined, need not to have the same polynomial degree.
NOTE 1 A B-spline surface compactly represents a large smooth area. However, if the shape is mainly smooth, but with some areas of higher complexity, the data size of a B-spline surface tends to be high. Due to the tensor product construction of the B-spline surface the knot lines are global and high data size in one area of the surface cannot be kept locally. The following approaches to define a B-spline surface with the property of local refinement have been pursued:
NOTE 2 A locally refined spline surface is rational if and only if the weights are not all identical; this can be represented by the rational_locally_refined_spline_surface subtype. If it is polynomial, the weights may be defaulted to all being 1.
Interpretation of the data is as follows: The surface, in the polynomial case, is given by:
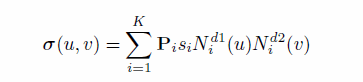

K = number of control points,
P i = control points(i),
si = scaling_factors(i),
wi = weights_data(i),
N i d1(u) = u_bspline(i), and
d1=u_degree.
N i d2(v) = v_bspline(i), and
d2=v_degree.
NOTE 2 The degrees are associated with the local_b_splines and do not need to be constant throughout the surface.
The weights, in the case of the rational subtype, are given in the same sequence as the coefficients. The knot values and multiplicities are defined in the entity local_b_spline. The B-splines are defined over a domain described by knot vectors in the parameter directions of the surface. However, in contrast to B-bspline surfaces, the basis functions or B-splines do not need to adapt to all knot lines in their supports. This facilitates the definition of a spline surface on a box partition.NOTE 3 When the polynomial degree is the same for all B-splines and no knot lines exist that do not cross the entire parameter domain, the locally_refined_spline_surface will coincide with b_spline_surface_with_knots. In that case b_spline_surface_with_knots. has the simplest and most compact representation.
NOTE 4 A locally_refined_spline_surface can be of type analysis suitable T-spline, hierarchical B-spline, LR-spline, semi standard T-spline or standard T-spline. The type is given by the enumeration locally_refined_spline_type_enum, and the packing and unpacking of the surface will depend on this type.
EXAMPLE The parameter domain of a locally refined spline surface illustrated as a regular mesh. The knot lines can have varying multiplicity throughout the domain. The numbers show the maximum multiplicity of each knot.There may exist B-splines with a given knot in its domain where this knot has a multiplicity less than the maximum multiplicity. Zero multiplicity indicates that this knot does not exist in that part of the domain. No B-splines have this knot in their definition. This mesh corresponds to a surface that is quadratic in both parameter directions for all local B-splines.
The locally refined spline surface contains two knot values lists, one for each parameter direction. The knot values are (0, 1.0, 1.5, 2.0, 3.0) in the first parameter (u) direction and (0.0, 1.0, 1.2, 1.8, 2.0, 3.0) in the second parameter direction.
The univariate B-splines in the first parameter direction are:
The univariate B-splines in the second parameter direction are:
Each control point is associated with the product of 2 B-splines one in u and one in v. The list of pairs of B-splines starts with all pairs of products of B-splines with knot values (0,0):
(1u.1v, 2u.1v, 5u.1v, 1u.3v, 2u.3v, 5u.3v 1u.6v, 2u.6v, 5u.6v).
The list continues with all the remaining B-spline products with first knot value v = 0 :
(8u.1v, 8u.2v, 8u.5v, 10u.1v, 10u.2v, 10u.5v, 11u.1v, 11u.2v, 11u.5v)
The list continues with all the B-spline products with first knot value v = 1
(1u.9v, 2u.9v, 5u.9v, 7u.7v, 11u.8v).
Finally we list all B-spline products with first knot values v = 2 and v = 4
(9u.10v, 11u.10v) and (1u.11v, 3u.11v, 6u.11v, 9u.11v, 11u.11v).
In this example the splines are of type LR B-spline and all scaling factors have value 1.0. Corresponding to the orders in the consecutive lists above the complete data defining the geometry of the curve is a list of 30 u_b_splines, a corresponding list of 30 v_b_splines, a list of 5 u_knots, a list of 6 v_knots, a list of 30 control points and a corresponding list of 30 scaling factors.
The combined B-splines are not tested for linearly independence. The domain is [0,3]x[0,3]. The surface_form is unspecified and the matter of self-intersection and whether the surface is closed in any direction depends on the control_points_list.
EXPRESS specification:
*)
ENTITY locally_refined_spline_surface
SUBTYPE OF (bounded_surface);
u_b_splines : LIST[4:?] OF local_b_spline;
v_b_splines : LIST[4:?] OF local_b_spline;
u_knots : spline_knot_values;
v_knots : spline_knot_values;
control_points_list : LIST[4:?] OF cartesian_point;
scaling_factors : LIST[4:?] OF REAL;
linearly_independent : linearly_independent_enum;
locally_refined_spline_type : locally_refined_spline_type_enum;
self_intersect : LOGICAL;
u_closed : LOGICAL;
v_closed : LOGICAL;
domain : LIST[2:2] OF LIST[2:2] OF REAL;
WHERE
WR1: SIZEOF(u_b_splines) = SIZEOF(control_points_list);
WR2: SIZEOF(v_b_splines) = SIZEOF(control_points_list);
WR3: SIZEOF(scaling_factors) = SIZEOF(control_points_list);
WR4: constraints_scaling(scaling_factors);
END_ENTITY;
(*
Attribute definitions:
u_b_splines: the local_b_spline functions in the first (u) parameter direction from which the surface is defined. These functions refer to the u_knots list for their knot parameter values;
v_b_splines: the local_b_spline functions in the second (v) parameter direction from which the surface is defined. These functions refer to the v_knots list for their knot parameter values;
NOTE 5 There may be some repetitions in the 2 lists of local_b_splines.
u_knots: the list of knot values for parameter u;
v_knots: the list of knot values for parameter v;
control_points_list: the list of control points. The control_points_list and consequently also the u_b_splines, the v_b_splines and scaling_factors, are ordered according to the knot values of the the combined B-spline coefficient constructed by multiplying corresponding univariate B-splines starting from the lowest knot value for each parameter. The knots in the v-parameter are the major sorting factor while the knots in the u-parameter the minor sorting factor. In case of ambiguities, the lists are sorted according to the upper knot value pair of the combined B-splines and the multiplicities of the first knots of the univariate B-splines.
scaling_factors: the list of scaling factors used to ensure that the non-zero B-spline basis functions add up to unity (partition of unity) at all points in the domain. Scaling factors not equal to 1.0 are sometimes needed for semi_standard_t_spline and lr_b_spline definitions to ensure that the collection of B-spline basis functions form a partition of unity. For analysis_suitable_t_spline and standard_t_spline definitions, partition of unity is achieved without use of scaling factors (i.e., the scaling factor is always equal to 1.0). For hierarchical_b_spline definitions, a scaling factor equal to 1.0 is used, although there is no partition of unity achieved.
linearly_independent: indicates whether this property has been tested for and in that case the result of the test; this is for information only;
NOTE 6 The test is applied to the set of products of local_b_splines used as coefficients of the control points . Not all types of locally refined surfaces are linearly independent by default.
locally_refined_spline_type: the type of the initial locally refined spline surface that provides rules for how the stored surface can be unpacked to its original format;
self_intersect: indication whether the surface is self-intersecting; this is for information only.
u_closed: indication whether the surface is closedin the u direction; this is for information only;
v_closed: indication whether the surface is closedin the v direction; this is for information only;
domain: the parameter domain corresponding to the surface. domain(1),(1) is the minimum parameter value in the u direction; domain(1),(2) is the maximum parameter value in the u direction; domain(2),(1) and domain (2),(2) gives the minimum and maximum parameter values in the v direction. If all B-splines at the boundary have a knot multiplicity equal to the degree+1 at this boundary, the domain will coincide with the domain given by the minimum and maximum values in u_knots and v_knots. Otherwise, it will be coincide with a domain given by nearby knots depending on knot multiplicities.
Formal propositions:
WR1: the number of u_b_splines shall be equal to the number of control points;
WR2: the number of v_b_splines shall be equal to the number of control points;
WR3: the number of scaling_factors shall be equal to the number of control points;
WR4: all scaling_factors shall be positive and not greater than 1.0.

A rational_locally_refined_spline_surface is a type of locally_refined_spline_surface that is a piecewise parametric rational surface described in terms of control points and local B-spline functions.
EXPRESS specification:
*)
ENTITY rational_locally_refined_spline_surface
SUBTYPE OF (locally_refined_spline_surface);
weights_data : LIST[4:?] OF REAL;
WHERE
WR1: SIZEOF(weights_data) = SIZEOF(SELF\locally_refined_spline_surface.
control_points_list);
WR2: weights_positive(weights_data);
END_ENTITY;
(*
Attribute definitions:
weights_data: the supplied values of the weights.
Formal propositions:
WR1: the size of the of weights_data list shall be equal to the number of control points
WR2: all values in the weights_data list shall be positive.

A rectangular_trimmed_surface is a type of bounded_surface, in which the boundaries are the constant parametric lines u1 = u1, u2 = u2, v1 = v1 and v2 = v2. All these values shall be within the parametric range of the referenced surface. Cyclic properties of the parameter range are assumed.
NOTE 1 For example, 370 degrees is equivalent to 10 degrees, for those surfaces whose parametric form is defined using circular functions (sine and cosine).
The rectangular trimmed surface inherits its parametrisation directly from the basis surface and has parameter ranges from 0 to |u2 - u1| and 0 to |v2 - v1|. The derivation of the new parameters from the old uses the algorithm described in trimmed_curve.NOTE 2 If the surface is closed in a given parametric direction, the values of >u or >v2 may require to be increased by the cyclic range.
EXPRESS specification:
*)
ENTITY rectangular_trimmed_surface
SUBTYPE OF (bounded_surface);
basis_surface : surface;
u1 : parameter_value;
u2 : parameter_value;
v1 : parameter_value;
v2 : parameter_value;
usense : BOOLEAN;
vsense : BOOLEAN;
WHERE
WR1: u1 <> u2;
WR2: v1 <> v2;
WR3: (('GEOMETRY_SCHEMA.ELEMENTARY_SURFACE' IN TYPEOF(basis_surface)) AND (NOT ('GEOMETRY_SCHEMA.PLANE' IN TYPEOF(basis_surface))))
OR ('GEOMETRY_SCHEMA.SURFACE_OF_REVOLUTION' IN TYPEOF(basis_surface)) OR (usense = (u2 > u1));
WR4: (('GEOMETRY_SCHEMA.SPHERICAL_SURFACE' IN TYPEOF(basis_surface)) OR ('GEOMETRY_SCHEMA.TOROIDAL_SURFACE' IN TYPEOF(basis_surface)))
OR (vsense = (v2 > v1));
END_ENTITY;
(*
Attribute definitions:
basis_surface: the surface being trimmed;
u1: the first u parametric value;
u2: the second u parametric value;
v1: the first v parametric value;
v2: the second v parametric value;
usense: a flag to indicate whether the direction of the first parameter of the trimmed surface agrees with or opposes the sense of u in the basis surface;
vsense: a flag to indicate whether the direction of the second parameter of the trimmed surface agrees with or opposes the sense of v in the basis surface.
Formal propositions:
WR1: The attributes u1 and u2 shall have different values.
WR2: The attributes v1 and v2 shall have different values.
WR3: With the exception of those surfaces closed in the u parameter direction, usense shall be compatible with the ordered parameter values for u.
WR4: With the exception of those svrfaces closed in the v parameter direction, vsense shall be compatible with the ordered parameter valves for v.
Informal propositions:
IP1: The domain of the trimmed surface shall be within the domain of the surface being trimmed.

A curve_bounded_surface is a type of bounded_surface, and is a parametric surface with curved boundaries defined by one or more boundary_curves or degenerate_pcurves. One of the boundary_curves may be the outer boundary; any number of inner boundaries is permissible. The outer boundary may be defined implicitly as the natural boundary of the surface; this is indicated by the implicit_outer flag being true. In this case at least one inner boundary shall be defined. For certain types of closed, or partially closed, surface (such as a cylinder) it may not be possible to identify any given boundary as outer. The region of the curve_bounded_surface in the basis_surface is defined to be the portion of the basis surface in the direction of n × t from any point on the boundary, where n is the surface normal and t the boundary curve tangent vector at this point. The region so defined shall be arcwise connected.
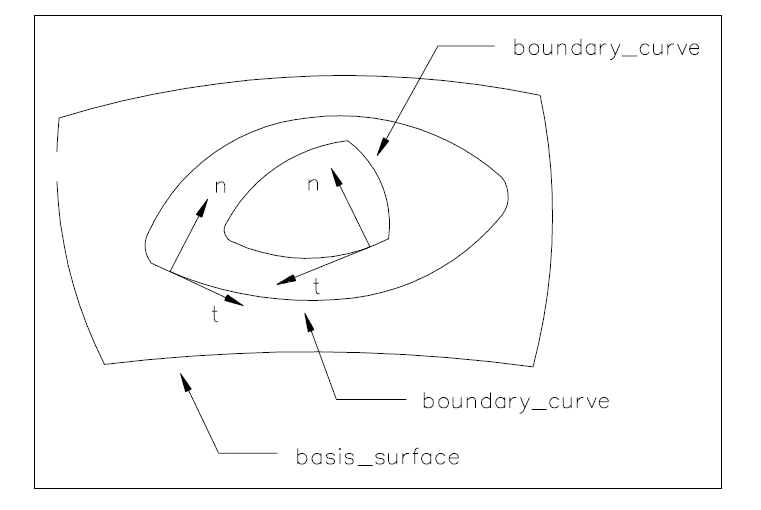
EXPRESS specification:
*)
ENTITY curve_bounded_surface
SUBTYPE OF (bounded_surface);
basis_surface : surface;
boundaries : SET[1:?] OF boundary_curve;
implicit_outer : BOOLEAN;
WHERE
WR1: (NOT implicit_outer) OR (SIZEOF (QUERY (temp <* boundaries | 'GEOMETRY_SCHEMA.OUTER_BOUNDARY_CURVE' IN TYPEOF(temp)))
= 0);
WR2: (NOT(implicit_outer)) OR ('GEOMETRY_SCHEMA.BOUNDED_SURFACE' IN TYPEOF(basis_surface));
WR3: SIZEOF(QUERY(temp <* boundaries | 'GEOMETRY_SCHEMA.OUTER_BOUNDARY_CURVE' IN TYPEOF(temp))) <= 1;
WR4: SIZEOF(QUERY(temp <* boundaries | (temp\composite_curve_on_surface.basis_surface [1] <> basis_surface))) = 0;
END_ENTITY;
(*
Attribute definitions:
basis_surface: the surface to be bounded;
boundaries: the bounding curves of the surface, other than the implicit outer boundary, if present; at most, one of these may be identified as an outer boundary by being of type outer_boundary_curve;
implicit_outer: a Boolean flag which, if true, indicates the natural boundary of the surface is used as an outer boundary.
NOTE See Figure (22) for interpretation of these attributes.
Formal propositions:
WR1: No explicit outer boundary shall be present when implicit_outer is TRUE.
WR2: The outer boundary shall only be implicitly defined if the basis_surface is bounded.
WR3: At most, one outer boundary curve shall be included in the set of boundaries.
WR4: Each boundary_curve shall lie on the basis_surface. This is verified from the basis_surface attribute of the composite_curve_on_surface supertype for each element of the boundaries list.
Informal propositions:
IP1: Each curve in the set of boundaries shall be closed.
IP2: No two curves in the set of boundaries shall intersect.
IP3: At most one of the boundary curves may enclose any other boundary curve. If an outer_boundary_curve is designated, only that curve may enclose any other boundary curve.

A boundary_curve is a type of composite_curve_on_surface suitable for the definition of a surface boundary.
EXPRESS specification:
*)
ENTITY boundary_curve
SUBTYPE OF (composite_curve_on_surface);
WHERE
WR1: SELF\composite_curve.closed_curve;
END_ENTITY;
(*
Formal propositions:
WR1: The derived closed_curve attribute of the composite_curve supertype shall be TRUE.

An outer_boundary_curve is a type of boundary_curve which has the additional semantics of defining an outer boundary of a surface. No more than one such curve shall be included in the set of boundaries of a curve_bounded_surface.
EXPRESS specification:
*)
ENTITY outer_boundary_curve
SUBTYPE OF (boundary_curve);
END_ENTITY;
(*

A rectangular_composite_surface is a type of bounded_surface composed of a rectangular array of n_u by n_v segments or patches. Each segment shall be finite and topologically rectangular (i.e., it corresponds to a rectangle in parameter space). The segment shall be either a b_spline_surface or a rectangular_trimmed_surface. There shall be at least positional continuity between adjacent segments in both directions; the composite surface may be open or closed in the u direction and open or closed in the v direction.
For a particular segment Sij = segments[i][j]:
The preceding segment in the u direction is S(i-1)j and the preceding segment in the v direction is Si(j-1) ; similarly for following segments.
If segments[i][j].u_sense is TRUE, the boundary of Sij where it adjoins S(i=1)j is that where the u parameter (of the underlying bounded surface) is high.
If segments[i][j].u_sense is FALSE, it is at the low u boundary; similarly for the v_sense indicator.
The u parametrisation of Sij in the composite surface is from i-1 to i, mapped linearly from the parametrisation of the underlying bounded surface.
If U is the u parameter for the rectangular_composite_surface and uij0 ≤ uijij ≤ uij1 , is the u parameter for segments[i][j], these parameters are related by the equations:
U = (i - 1) + (uij - uij0)/(uij1 - uij0), uij = uij0 + (U -(i-1))(uij1 - uij0),
if segments[i][j].u_sense = TRUE;
U = i - (uij - uij0)/(uij1 - uij0), uij = uij0 - (U -i)(uij1 - uij0),
if segments[i][j].u_sense = FALSE.
The v parametrisation is obtained in a similar way.
Thus the composite surface has parametric range 0 to n_u, 0 to n_v.
The degree of continuity of the joint between Sij and S(i+1)j/ is given by segments[i][j].u_transition.
For the last patch in a row S(n_u)j this may take the value discontinuous, if the composite surface is open in the u direction; otherwise it is closed here, and the transition code relates to the continuity to S1j ; similarly for v_transition. discontinuous shall not occur elsewhere in the segments surface_patch transition codes.
EXPRESS specification:
*)
ENTITY rectangular_composite_surface
SUBTYPE OF (bounded_surface);
segments : LIST[1:?] OF LIST[1:?] OF surface_patch;
DERIVE
n_u : INTEGER := SIZEOF(segments);
n_v : INTEGER := SIZEOF(segments[1]);
WHERE
WR1: SIZEOF(QUERY (s <* segments | n_v <> SIZEOF (s))) = 0;
WR2: constraints_rectangular_composite_surface(SELF);
END_ENTITY;
(*
Attribute definitions:
segments: a rectangular array (represented by a list of list) of component surface patches. Each such patch contains information on the senses and transitions.
segments[i][j].u_transition refers to the state of continuity between segments[i][j] and segments[i+1][j]. The last column (segments[n_u][j].u_transition) may contain the value discontinuous, meaning that (that row of) the surface is not closed in the u direction; the rest of the list shall not contain this value.
The last row (segments[i][n_v].v_transition) may contain the value discontinuous, meaning that (that column of) the surface is not closed in the v direction; the rest of the list shall not contain this value.
n_u: the number of surface oatches in the u parameter direction;
n_v: the number of surface oatches in the v parameter direction.
Formal propositions:
WR1: Each sub-list in the segments list shall contain n_v surface_patches.
WR2: Other constraints on the segments (veriofied by constraints_rectangular_composite_surface function are:
that the component surfaces are all either rectangular trimmed surfaces or B-spline surfaces;
that the transition_codes in the segments list do not contain the value discontinuous except for the last row or column; when this occurs, it indicates that the surface is not closed in the appropriate direction.
Informal propositions:
IP1: The senses of the component surfaces are as specified in the u_sense and v_sense attributes of each element of segments.

A surface_patch is a type of founded_item and is a bounded surface with additional transition and sense information which is used to define a rectangular_composite_surface.
EXPRESS specification:
*)
ENTITY surface_patch
SUBTYPE OF (founded_item);
parent_surface : bounded_surface;
u_transition : transition_code;
v_transition : transition_code;
u_sense : BOOLEAN;
v_sense : BOOLEAN;
INVERSE
using_surfaces : BAG[1:?] OF rectangular_composite_surface FOR segments;
WHERE
WR1: (NOT ('GEOMETRY_SCHEMA.CURVE_BOUNDED_SURFACE' IN TYPEOF(parent_surface)));
END_ENTITY;
(*
Attribute definitions:
parent_surface: the surface which defines the geometry and boundaries of the surface patch;
NOTE Since surface_patch is not a subtype of geometric_representation_item the instance of bounded_surface used as parent_surface is not automatically associated with the geometric_representation_context of the representation using a rectangular_composite_surface containing this surface_patch. It is therefore necessary to ensure that the bounded_surface instance is explicitly included in a representation with the appropriate geometric_representation_context.
u_transition: the minimum state of geometric continuity along the second u boundary of the patch as it joins the first u boundary of its neighbour. In the case of the last patch, this defines the state of continuity between the first u boundary and last u boundary of the rectangular_composite_surface;
v_transition: the minimum state of geometric continuity along the second v boundary of the patch as it joins the first v boundary of its neighbour. In the case of the last patch, this defines the state of continuity between the first v boundary and last v boundary of the rectangular_composite_surface;
u_sense: the relationship between the sense (increasing parameter value) of the patch and the sense of the parent_surface. If u_sense is TRUE, the first u boundary of the patch is the one where the parameter u takes its lowest value; it is the highest value boundary if sense is FALSE.
v_sense: the relationship between the sense (increasing parameter value) of the patch and the sense of the parent_surface. If v_sense is TRUE, the first v boundary of the patch is the one where the parameter v takes its lowest value; it is the highest value boundary if sense is FALSE.
using_surfaces: the bag of rectangular_composite_surfaces which use this surface_patch in their definition. This bag shall not be empty.
Formal propositions:
WR1: A curve bounded surface shall not be used to define a surface patch.

A offset_surface is a type of surface and is a procedural definition of a simple offset surface at a normal distance from the originating surface. distance may be positive, negative or zero to indicate the preferred side of the surface. The positive side and the resultant offset surface are defined as follows:
Define unit tangent vectors of the base surface in the u and v directions; denote these by σ u and σ v .
Take the cross product, N = σ u × σ v , of these (which shall be linearly independent, or there is no offset surface).
N shall be extended by continuity at singular points, if possible.
Normalise N to get a unit normal (to the surface) vector.
Move the offset distance (which may be zero) along that vector to find the point on the offset surface.
NOTE 1 The definition allows the offset_surface to be self-intersecting.
The offset surface takes its parametrisation directly from that of the basis surface, corresponding points having identical parameter values. The offset_surface is parametrised as
σ(u,v) = S(u,v) + dN.
Where N is the unit normal vector to the basis surface S(u,v) at parameter values (u,v), and d is distance.
NOTE 2 Care should be taken when using this entity to ensure that the offset distance never exceeds the radius of curvature in any direction at any point of the basis surface. In particular, the surface should not contain any ridge or singular point.
EXPRESS specification:
*)
ENTITY offset_surface
SUBTYPE OF (surface);
basis_surface : surface;
distance : length_measure;
self_intersect : LOGICAL;
END_ENTITY;
(*
Attribute definitions:
basis_surface: the surface that is to be offset;
distance: the offset distance, which may be positive, negative or zero. A positive offset distance is measured in the direction of the surface normal;
self_intersect: a flag to indicate whether or not the surface is self-intersecting; this is for information only.

A oriented_surface is a type of surface for which the direction of the surface normal may be reversed.
The unit normal N, at any point on the oriented_surface is defined by the eqations:
N (u,v) = < ((∂σ)/(∂ u) × (∂σ)/(∂ v)) > , if orientation = .TRUE.,
N (u,v) = - < ((∂σ)/(∂ u) × (∂σ)/(∂ v)) > , if orientation = .FALSE.,
NOTE An oriented_surface may be instantiated with other subtypes of surface. For example a complex instance of oriented_surface, with orientation = .FALSE., and spherical_surfacedefines a spherical surface with an inward pointing normal.
EXPRESS specification:
*)
ENTITY oriented_surface
SUBTYPE OF (surface);
orientation : BOOLEAN;
END_ENTITY;
(*
Attribute definitions:
orientation: a flag which indicates whether, or not, the direction of the surface normal is reversed.

A surface_replica is a type of surface which defines a replica of an existing surface in a different location. It is defined by referencing the parent surface and a transformation which gives the new position and possible scaling. The original surface is not affected. The geometric characteristics of the surface produced will be identical to that of the parent surface, but, where the transformation includes scaling, the size may differ.
EXPRESS specification:
*)
ENTITY surface_replica
SUBTYPE OF (surface);
parent_surface : surface;
transformation : cartesian_transformation_operator_3d;
WHERE
WR1: acyclic_surface_replica(SELF, parent_surface);
END_ENTITY;
(*
Attribute definitions:
parent_surface: the surface that is being copied;
transformation: the cartesian_transformation_operator_3d which defines the location, orientation and scaling of the surface replica relative to that of the parent surface.
Formal propositions:
WR1: A surface_replica shall not participate in its own definition.

A volume is a type of geometric_representation_item that is a three dimensional solid of finite volume with a tri-parametric representation.
Each volume has a parametric representationV (u,v,w)
where u, v, w are independent dimensionless parameters. For each (u,v,w) within the parameter range:
r = V (u,v,w),
gives the coordinates of a point within the volume.
NOTE In this version of the standard the parameter ranges for the standard primitives have been standardised, mainly to [0:1], to ensure that they are dimensionless quantities.
EXPRESS specification:
*)
ENTITY volume
SUPERTYPE OF (ONEOF (block_volume,
wedge_volume,
spherical_volume,
cylindrical_volume,
eccentric_conical_volume,
toroidal_volume,
pyramid_volume,
b_spline_volume,
ellipsoid_volume,
tetrahedron_volume,
hexahedron_volume,
locally_refined_spline_volume))
SUBTYPE OF (geometric_representation_item);
WHERE
WR1: SELF\geometric_representation_item.dim = 3;
END_ENTITY;
(*
Formal propositions:
WR1: The coordinate space dimensionality shall be 3.

A block_volume is a type of volume in the form of a solid rectangular parallelepiped, defined with a location and placement coordinate system. The block_volume is specified by the positive lengths x, >y, and z along the axes of the placement coordinate system, and has one vertex at the origin of the placement coordinate system.
The data is to be interpreted as follows:
C = position.location (corner)
x = position.p[1]
y = position.p[2]
z = position.p[3]
l =x (length)
d = y (depth)
h = z (height)
and the volume is parametrised as:
V(u,v,w) = C + ul x + vd y + wh z
where the parametrisation range is 0 ≤ u ≤ 1, 0 ≤ v ≤ 1 , and 0 ≤ w ≤ 1.
EXPRESS specification:
*)
ENTITY block_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
x : positive_length_measure;
y : positive_length_measure;
z : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
position: the location and orientation of the axis system for the primitive. The block has one vertex at position.location and its edges aligned with the placement axes in the positive sense;
x: the size of the block along the placement X axis, (position.p[1]);
y: the size of the block along the placement Y axis, (position.p[2]);
z: the size of the block along the placement Z axis, (position.p[3]).

A wedge_volume is a type of volume which can be envisioned as the result of intersecting a block with a plane perpendicular to one of its faces. It is defined with a location and local coordinate system. A triangular/trapezoidal face lies in the plane defined by the placement X and Y axes. This face is defined by positive lengths x and y along the placement X and Y axes, by the length ltx (if non-zero) parallel to the X axis at a distance y from the placement origin, and by the line connecting the ends of the x and ltx segments.
The remainder of the wedge is specified by the positive length z along the placement Z axis which defines a distance through which the trapezoid or triangle is extruded. If ltx= 0, the wedge has five faces; otherwise, it has six faces.
NOTE See Figure (23) for interpretation of attributes.
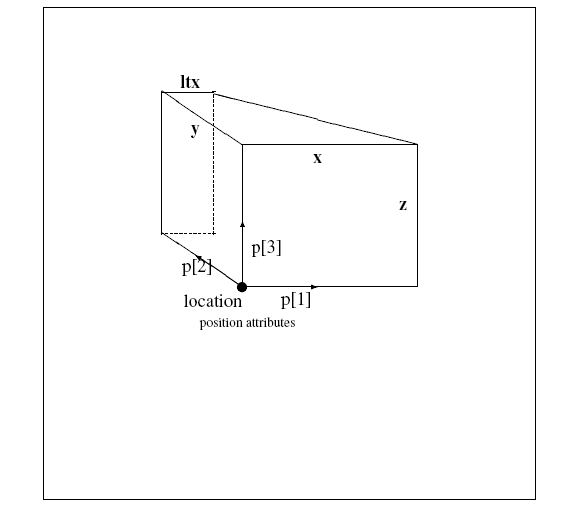
The data is to be interpreted as follows:
C = position.location (corner)
x = position.p[1]
y = position.p[2]
z = position.p[3]
l =x (length)
d = y (depth)
h = z (height)
lmin =ltxx (length)
and the volume is parametrised as:
V(u,v,w) = C + u((1 - v)l + vlmin) x + vd y + wh z
where the parametrisation range is 0 ≤ u ≤ 1, 0 ≤ v ≤ 1 , and 0 ≤ w ≤ 1.
EXPRESS specification:
*)
ENTITY wedge_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
x : positive_length_measure;
y : positive_length_measure;
z : positive_length_measure;
ltx : length_measure;
WHERE
WR1: ((0.0 <= ltx) AND (ltx < x));
END_ENTITY;
(*
Attribute definitions:
position: the location and orientation of the axis system for the primitive. The wedge has one vertex at position.location and its edges aligned with the placement axes in the positive sense;
x: the size of the wedge along the placement X axis, (position.p[1]);
y: the size of the wedge along the placement Y axis, (position.p[2]);
z: the size of the wedge along the placement Z axis, (position.p[3]);
ltx: the length in the positive X direction of the smaller surface of the wedge.
Formal propositions:
WR1: The attribute ltx shall be non-negative and less than x.

A pyramid_volume is a type of volume in the form of a solid pyramid with a rectangular base. The apex of the pyramid is directly above the centre point of the base. The pyramid_volume is specified by its position, which provides a placement coordinate system, its length, depth and height.
The data is to be interpreted as follows:
C = position.location (corner)
x = position.p[1]
y = position.p[2]
z = position.p[3]
l =xlength
d = ydepth
h = height
and the volume is parametrised as:
V(u,v,w) = C + w((l/2) x + (d/2) y + h z) + (1 - w)(ul x + vd y)
where the parametrisation range is 0 ≤ u ≤ 1, 0 ≤ v ≤ 1 , and 0 ≤ w ≤ 1.
EXPRESS specification:
*)
ENTITY pyramid_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
xlength : positive_length_measure;
ylength : positive_length_measure;
height : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
position: the location and orientation of the pyramid. position defines a placement coordinate system for the pyramid; the pyramid has one corner of its base at position.location and the edges of the base are aligned with the first two placement axes in the positive sense;
xlength: the length of the base measured along the placement X axis (position.p[1]);
ylength: the length of the base of the pyramid along the placement Y axis, (position.p[2]);
height: the height of the apex above the plane of the base, measured in the direction of the placement Z axis, (position.p[3]).

A tetrahedron_volume is a type of volume with 4 vertices and 4 triangular faces. It is defined by the four cartesian_points which locate the vertices. These points shall not be coplanar.
The data is to be interpreted as follows:
a = point_1.coordinates
b = point_2.coordinates
c = point_3.coordinates
d = point_4.coordinates
and the volume is parametrised as:
V(u,v,w) = a + u(b - a) + v(c - a) + w(d - a)
where the parametrisation range is 0 ≤ u ≤ 1, 0 ≤ v ≤ 1 , and 0 ≤ w ≤ 1, with u + v + w ≤ 1.
EXPRESS specification:
*)
ENTITY tetrahedron_volume
SUBTYPE OF (volume);
point_1 : cartesian_point;
point_2 : cartesian_point;
point_3 : cartesian_point;
point_4 : cartesian_point;
WHERE
WR1: point_1.dim = 3;
WR2: above_plane(point_1, point_2, point_3, point_4) <> 0.0;
END_ENTITY;
(*
Attribute definitions:
point_1: the cartesian_point that locates the first vertex of the tetrahedron_volume;
point_2: the cartesian_point that locates the second vertex of the tetrahedron_volume;
point_3: the cartesian_point that locates the third vertex of the tetrahedron_volume;
point_4: the cartesian_point that locates the fourth vertex of the tetrahedron_volume.
Formal propositions:
WR1: The coordinate space dimension of point_1 shall be 3.
NOTE The rule compatible_dimension ensures that all the cartesian_point attributes of this entity have the same dimension.
WR2: The points point_1, point_2, point_3 and point_4 shall not be coplanar. This is tested by verifying that the cross_product of the three directions from point_1 to each of the other points is non-zero.

A hexahedron_volume is a type of volume with 8 vertices and 6 four-sided faces. It is defined by the 8 points which locate the vertices. The volume is parametrised as
V (u,v,w) = (1 - u)(1 - v)(1 - w) P1 + (1 - u)(v)(1 -w) P2 + uv(1 - w) P3 + u(1 -v)(1 - w) P4 + (1 - u)(1 - v)w P5 + (1 - u)(v)w P6 + uvw P7 + u(1 -v)w P8
where the parametrisation range is 0 ≤ u ≤ 1, 0 ≤ v ≤ 1 , and 0 ≤ w ≤ 1. and P i denotes the position vector of points[i]
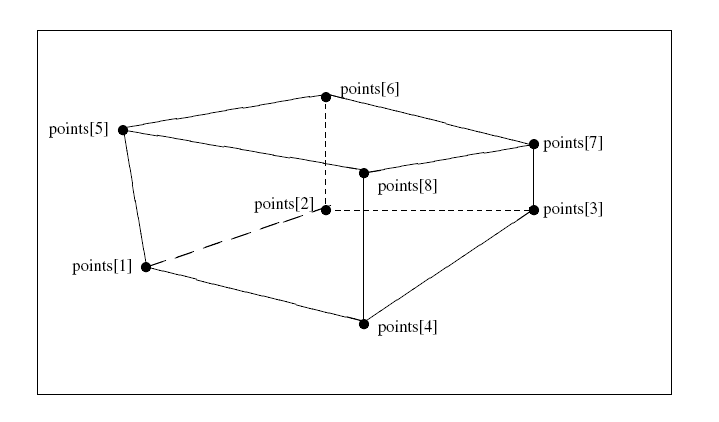
EXPRESS specification:
*)
ENTITY hexahedron_volume
SUBTYPE OF (volume);
points : LIST[8:8] OF cartesian_point;
WHERE
WR1: above_plane(points[1], points[2], points[3], points[4]) = 0.0;
WR2: above_plane(points[5], points[8], points[7], points[6]) = 0.0;
WR3: above_plane(points[1], points[4], points[8], points[5]) = 0.0;
WR4: above_plane(points[4], points[3], points[7], points[8]) = 0.0;
WR5: above_plane(points[3], points[2], points[6], points[7]) = 0.0;
WR6: above_plane(points[1], points[5], points[6], points[2]) = 0.0;
WR7: same_side([points[1], points[2], points[3]], [points[5], points[6], points[7], points[8]]);
WR8: same_side([points[1], points[4], points[8]], [points[3], points[7], points[6], points[2]]);
WR9: same_side([points[1], points[2], points[5]], [points[3], points[7], points[8], points[4]]);
WR10: same_side([points[5], points[6], points[7]], [points[1], points[2], points[3], points[4]]);
WR11: same_side([points[3], points[7], points[6]], [points[1], points[4], points[8], points[5]]);
WR12: same_side([points[3], points[7], points[8]], [points[1], points[5], points[6], points[2]]);
WR13: points[1].dim = 3;
END_ENTITY;
(*
Attribute definitions:
points: the cartesian_points that locate the vertices of the hexahedron_volume. These points are ordered such that points[1], points[2], points[3], points[4] define, in anti-clockwise order, one planar face of the solid and, in corresponding order.
points[5], points[6], points[7], points[8] define the opposite face.
NOTE 1 See Figure (24) for further information about the positions of the vertices.
Formal propositions:
WR1: The first 4 points shall be coplanar.
WR2: The final 4 points shall be coplanar.
WR3: The points points[1], points[4], points[8], points[5], shall be coplanar.
WR4: The points points[4], points[3], points[7], points[8], shall be coplanar..
WR5: The points points[3], points[2], points[6], points[7], shall be coplanar.
WR6: The points points[1], points[5], points[6], points[2], shall be coplanar.
WR7: The points points[5], points[6], points[7], points[8], shall all lie on the same side of the plane of points[1], points[2], points[3].
WR8: The points points[3], points[7], points[6], points[2], shall all lie on the same side of the plane of points[1], points[4], points[8].
WR9: The points points[4], points[3], points[7], points[8], shall all lie on the same side of the plane of points[1], points[2], points[5].
WR10: The points points[1], points[2], points[3], points[4], shall all lie on the same side of the plane of points[5], points[6], points[7].
WR11: The points points[1], points[4], points[8], points[5], shall all lie on the same side of the plane of points[3], points[7], points[6].
WR12: The points points[1], points[5], points[6], points[2], shall all lie on the same side of the plane of points[3], points[7], points[8].
NOTE 2 The above 6 rules ensure that the points define a convex figure.
WR13: The point points[1] shall have coordinate space dimensionality 3.

A spherical_volume is a type of volume in the form of a sphere of radius R. A spherical_volume is defined by the radius and the position of the solid.
The data is to be interpreted as follows:
C = position.location (centre)
x = position.p[1]
y = position.p[2]
z = position.p[3]
R =radius
and the volume is parametrised as:
V (u,v,w) = C + wRcos((πv)/2)((cos(2πu)) x + (sin(2πu)) y) + wR(sin ((πv)/2)) z
where the parametrisation range is 0 ≤ u ≤ 1, -1 ≤ v ≤ 1 , and 0 ≤ w ≤ 1.where the parametrisation range is 0 ≤ u ≤ 1, 0 ≤ v ≤ 1 , and 0 ≤ w ≤ 1.
EXPRESS specification:
*)
ENTITY spherical_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
radius : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
position: the location and parametric orientation of the volume; position.location is the centre of the sphere;
radius: the radius of the sphere.

A cylindrical_volume is a type of volume in the form of a circular cylinder. A cylindrical_volume is defined by its orientation and location, its radius and its height.
The data is to be interpreted as follows:
C = position.location
x = position.p[1]
y = position.p[2]
z = position.p[3]
R =radius
h =height
and the volume is parametrised as:
V (u,v,w) = C + wR((cos (2πu)) x + (sin(2πu) y) + vH z
where the parametrisation range is 0 ≤ u ≤ 1, 0 ≤ v ≤ 1 , and 0 ≤ w ≤ 1 .
EXPRESS specification:
*)
ENTITY cylindrical_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
radius : positive_length_measure;
height : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
position: the location and orientation of the cylinder; position.location is a point on the axis of the cylinder, and position.p{3] is the direction of the axis of the cylinder;
radius: the radius of the cylinder;
height: the height of the cylinder.

A eccentric_conical_volume is a type of volume in the form of a skew cone. The eccentric_conical_volume may have an elliptic cross section, and may have a central axis which is not perpendicular to the base. Depending upon the value of the ratio attribute it may be truncated, or may take the form of a generalised cylinder. When truncated the top face of the cone is parallel to the plane of the base and has a similar cross section.
The data is to be interpreted as follows:
C = position.location
x = position.p[1]
y = position.p[2]
z = position.p[3]
R1 = semi_axis_1
R2 = semi_axis_2
H = height
xo = x_offset
yo = y_offset
s = ratio
and the volume is parametrised as:
V (u,v,w) = C + v(xo x + yo y)+ w(1 + v(s - 1))( R1((2πu)) x + R2 (sin(2πu) y)) + vH z
where the parametrisation range is 0 ≤ u ≤ 1, 0 ≤ v ≤ 1 , and 0 ≤ w ≤ 1 .
NOTE 1 In the placement coordinate system defined by position the central point of the top face of the eccentric_conical_volume has coordinates (x_offset, y_offset, height).
NOTE 2 If ratio = 0.0 the eccentric_conical_volume includes the apex. If ratio = 1.0 the eccentric_conical_volume is in the form of a generalised cylinder with all cross sections of the same dimensions.
NOTE 3 If x_offset = y_offset = 0.0 the eccentric_conical_volume has the form of a right elliptic cone or, with R1 = R2 , a right circular cone.
EXPRESS specification:
*)
ENTITY eccentric_conical_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
semi_axis_1 : positive_length_measure;
semi_axis_2 : positive_length_measure;
height : positive_length_measure;
x_offset : length_measure;
y_offset : length_measure;
ratio : REAL;
WHERE
WR1: ratio >= 0.0;
END_ENTITY;
(*
Attribute definitions:
position: the location of the central point on the axis and the direction of semi_axis_1; this defines the centre and plane of the base of the eccentric_conical_volume. position.p[3] is normal to the base of the eccentric_conical_volume;
semi_axis_1: the length of the first radius of the base of the cone in the direction of position.p[1];
semi_axis_2: the length of the second radius of the base of the cone in the direction of position.p[2];
height: the height of the cone above the base measured in the direction of position.p[3];
x_offset: the distance, in the direction of position.p[1], from the central point of the top face of the cone to the point in the plane of this face directly above the central point of the base;
y_offset: the distance, in the direction of position.p[2], from the central point of the top face of the cone to the point in the plane of this face directly above the central point of the base;
ratio: the ratio of a radius of the top face to the corresponding radius of the base of the cone.
Formal propositions:
WR1: The ratio shall not be negative.

A toroidal_volume is a type of volume which could be produced by revolving a circular face about a line in its plane. The radius of the circle being revolved is referred to here as the minor_radius and the major_radius is the distance from the centre of this circle to the axis of revolution. A toroidal_volume is defined by the major and minor radii and the position and orientation of the volume.
The data is to be interpreted as follows:
C = position.location
x = position.p[1]
y = position.p[2]
z = position.p[3]
R = major_radius
r = minor_radius
and the volume is parametrised as:
V (u,v,w) = C + (R + wrcos(2πv))((cos(2πu)) x + (sin(2πu)) y) + wr(sin(πv)) z
where the parametrisation range is 0 ≤ u ≤ 1, 0 ≤ v ≤ 1 , and 0 ≤ w ≤ 1 .
EXPRESS specification:
*)
ENTITY toroidal_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
major_radius : positive_length_measure;
minor_radius : positive_length_measure;
WHERE
WR1: minor_radius < major_radius;
END_ENTITY;
(*
Attribute definitions:
position: the location and orientation of the solid, position.location is the central point of the torus;
major_radius: the major radius of the torus;
minor_radius: the minor radius of the torus.
Formal propositions:
WR1: The minor radius shall be less than the major radius. This ensures that the parametric coordinates are unique for each point inside the volume.

A ellipsoid_volume is a type of volume in the form of a solid ellipsoid. It is defined by its location and orientation and by the lengths of the three semi-axes.
The data is to be interpreted as follows:
C = position.location (centre)
x = position.p[1]
y = position.p[2]
z = position.p[3]
a = semi_axis_1
b = semi_axis_2
c = semi_axis_3
and the volume is parametrised as:
V (u,v,w) = C + wcos((πv)/2) (a(cos(πu)) x + b(sin(2πu)) y) + wc(sin ((πv)/2)) z
where the parametrisation range is 0 ≤ u ≤ 1, 0 ≤ v ≤ 1 , and 0 ≤ w ≤ 1 .
EXPRESS specification:
*)
ENTITY ellipsoid_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
semi_axis_1 : positive_length_measure;
semi_axis_2 : positive_length_measure;
semi_axis_3 : positive_length_measure;
END_ENTITY;
(*
Attribute definitions:
position: the location and orientation of the ellipsoid. position.location is a cartesian_point at the centre of the ellipsoid and the axes of the ellipsoid are aligned with the directions position.p;
semi_axis_1: the length of the semi-axis of the ellipsoid in the direction position.p[1];
semi_axis_2: the length of the semi-axis of the ellipsoid in the direction position.p[2];
semi_axis_3: the length of the semi-axis of the ellipsoid in the direction position.p[3].

A b_spline_volume is a type of volume that is a general form of tri-parametric volume field which is represented by control points and basis functions. As with the B-spline curve and surface entities it has special subtypes where some of the data can be derived.
The data is to be interpreted as follows:
K1 = upper_index_on_u_control_values
K2 = upper_index_on_v_control_values
K2 = upper_index_on_v_control_values
P ijk = control_values
d1 = u_degree
d2 = v_degree
d3 = w_degree
The control values are ordered as
P 000, P 001, P 002, . . . , P K1K2(K3-1), P K1K2K3
For each parameter, s = u or v, or w if k is the upper index on the control points and d is the degree for s, the knot array is an array of (k + d + 2) real numbers [s-d, ... ,sk+1],
such that for all indices j in [-d, k], sj ≤ sj+1 .
This array is obtained from the appropriate knots_data list by repeating each multiple knot according to the multiplicity.
Ni d , the ith normalised B-spline basis function of degree d, is defined on the subset:
[si-d, ... ,si+1] of this array.
Let L denote the number of distinct values amongst the knots in the knot list; L will be referred to as the `upper index on knots'. Let mj denote the multiplicity (i.e., number of repetitions) of the jth distinct knot value. Then:
ΣL i=1 mi = d + k + 2
All knot multiplicities except the first and the last shall be in the range 1 .... d; the first and last may have a maximum value of d + 1.
NOTE In evaluating the basis functions, a knot u of, for example, multiplicity 3 is interpreted as a sequence u, u, u, in the knot array.
The parametric volume is given by the equation:
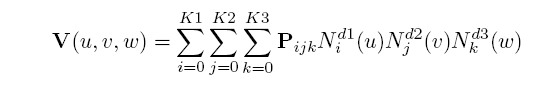
EXPRESS specification:
*)
ENTITY b_spline_volume
SUPERTYPE OF (ONEOF (b_spline_volume_with_knots,
uniform_volume,
quasi_uniform_volume,
bezier_volume)
ANDOR rational_b_spline_volume)
SUBTYPE OF (volume);
u_degree : INTEGER;
v_degree : INTEGER;
w_degree : INTEGER;
control_points_list : LIST[2:?] OF LIST[2:?] OF LIST[2:?] OF cartesian_point;
DERIVE
u_upper : INTEGER := SIZEOF(control_points_list) - 1;
v_upper : INTEGER := SIZEOF(control_points_list[1]) - 1;
w_upper : INTEGER := SIZEOF(control_points_list[1][1]) - 1;
control_points : ARRAY[0:u_upper] OF ARRAY[0:v_upper] OF ARRAY[0:w_upper] OF cartesian_point := make_array_of_array_of_array (control_points_list, 0,u_upper,0,v_upper, 0,w_upper );
WHERE
WR1: ('GEOMETRY_SCHEMA.BEZIER_VOLUME' IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.UNIFORM_VOLUME' IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.QUASI_UNIFORM_VOLUME'
IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.B_SPLINE_VOLUME_WITH_KNOTS' IN TYPEOF(SELF));
END_ENTITY;
(*
Attribute definitions:
u_degree: the algebraic degree of basis functions in u;
v_degree: the algebraic degree of basis functions in v;
w_degree: the algebraic degree of basis functions in w;
control_points_list: a list of lists of lists of control values;
u_upper: the upper index on control values in u direction;
v_upper: the upper index on control values in v direction;
w_upper: the upper index on control values in w direction;
control_points: the array (three-dimensional) of control values defining field geometry. This array is constructed from the control values list.
Formal propositions:
WR1: Any instantiation of this entity shall include one of the subtypes b_spline_volume_with_knots, or bezier_volume, or uniform_volume, or quasi_uniform_volume.

A b_spline_volume_with_knots is a type of b_spline_volume in which the knot values are explicitly given. This subtype shall be used to represent non-uniform B-spline volumes, and may also be used for other knot types.
All knot multiplicities except the first and the last shall be in the range 1 .... degree; the first and last may have a maximum value of degree + 1.
NOTE In evaluating the basis functions, a knot u of, for example, multiplicity 3 is interpreted as a sequence u, u, u, in the knot array.
EXPRESS specification:
*)
ENTITY b_spline_volume_with_knots
SUBTYPE OF (b_spline_volume);
u_multiplicities : LIST[2:?] OF INTEGER;
v_multiplicities : LIST[2:?] OF INTEGER;
w_multiplicities : LIST[2:?] OF INTEGER;
u_knots : LIST[2:?] OF parameter_value;
v_knots : LIST[2:?] OF parameter_value;
w_knots : LIST[2:?] OF parameter_value;
DERIVE
knot_u_upper : INTEGER := SIZEOF(u_knots);
knot_v_upper : INTEGER := SIZEOF(v_knots);
knot_w_upper : INTEGER := SIZEOF(w_knots);
WHERE
WR1: constraints_param_b_spline(SELF\b_spline_volume.u_degree, knot_u_upper, SELF\b_spline_volume.u_upper, u_multiplicities,
u_knots);
WR2: constraints_param_b_spline(SELF\b_spline_volume.v_degree, knot_v_upper, SELF\b_spline_volume.v_upper, v_multiplicities,
v_knots);
WR3: constraints_param_b_spline(SELF\b_spline_volume.w_degree, knot_w_upper, SELF\b_spline_volume.w_upper, w_multiplicities,
w_knots);
WR4: SIZEOF(u_multiplicities) = knot_u_upper;
WR5: SIZEOF(v_multiplicities) = knot_v_upper;
WR6: SIZEOF(w_multiplicities) = knot_w_upper;
END_ENTITY;
(*
Attribute definitions:
u_multiplicities: the multiplicities of the knots in the u parameter direction;
v_multiplicities: the multiplicities of the knots in the v parameter direction;
w_multiplicities: the multiplicities of the knots in the w parameter direction;
u_knots: the list of the distinct knots in the u parameter direction;
v_knots: the list of the distinct knots in the v parameter direction;
w_knots: the list of the distinct knots in the w parameter direction;
knot_u_upper: the number of distinct knots in the u parameter direction;
knot_v_upper: the number of distinct knots in the v parameter direction;
knot_w_upper: the number of distinct knots in the w parameter direction.
Formal propositions:
WR1: The function constraints_param_b_spline returns TRUE when the parameter constraints are verified for the u-direction.
WR2: The function constraints_param_b_spline returns TRUE when the parameter constraints are verified for the v-direction.
WR3: The function constraints_param_b_spline returns TRUE when the parameter constraints are verified for the w-direction.
WR4: The number of u_multiplicities shall be the same as the number of u_knots.
WR5: The number of v_multiplicities shall be the same as the number of v_knots.
WR6: The number of w_multiplicities shall be the same as the number of w_knots.

A bezier_volume is a type of b_spline_volume in which the knots are evenly spaced and have high multiplicities. Suitable default values for the knots and knot multiplicities are derived in this case. In this subtype the knot spacing is 1.0, starting from 0.0
NOTE If explicit knot values for the volume are required, they can be derived as follows:
ku_up := (SELF\backslash b_spline_volume.u_upper)/(SELF\backslash b_spline_volume.u_degree + 1)
kv_up := (SELF\backslash b_spline_volume.v_upper)/(SELF\backslash b_spline_volume.v_degree + 1)
kw_up := (SELF\backslash b_spline_volume.w_upper)/(SELF\backslash b_spline_volume.w_degree + 1)
ku_up is the value required for the upper index on the knot and knot multiplicity lists in the u direction. This is computed from the degree and the number of control values in this direction.
Similar computations are used to determine kv_up, kw_up.
The knot multiplicities and knots in the u, v and w parameter directions are then given by the function calls:
default_b_spline_knot_mult(SELF\b_spline_volume.u_degree, ku_up, bezier_knots)
default_b_spline_knots(SELF\b_spline_volume.u_degree,ku_up, bezier_knots)
default_b_spline_knot_mult(SELF\b_spline_volume.v_degree, kv_up, bezier_knots)
default_b_spline_knots(SELF\b_spline_volume.v_degree,kv_up, bezier_knots)
default_b_spline_knot_mult(SELF\b_spline_volume.w_degree, kw_up, bezier_knots)
default_b_spline_knots(SELF\b_spline_volume.w_degree,kw_up, bezier_knots)
EXPRESS specification:
*)
ENTITY bezier_volume
SUBTYPE OF (b_spline_volume);
END_ENTITY;
(*

A uniform_volume is a type of b_spline_volume in which the knots are evenly spaced. Suitable default values for the knots and knot multiplicities can be derived in this case.
A B-spline is {uniform if and only if all knots are of multiplicity 1 and they differ by a positive constant from the preceding knot. In this subtype the knot spacing is 1.0, starting from -degree.
NOTE If explicit knot values for the volume are required, they can be derived as follows:
ku_up := SELF\backslash b_spline_volume.u_upper + SELF\backslash b_spline_volume.u_degree + 2
kv_up := SELF\backslash b_spline_volume.u_upper + SELF\backslash b_spline_volume.v_degree + 2
kw_up := SELF\backslash b_spline_volume.u_upper + SELF\backslash b_spline_volume.w_degree + 2
ku_up is the value required for the upper index on the knot and knot multiplicity lists in the u direction. This is computed from the degree and the number of control values in this direction.
Similar computations are used to determine kv_up, kw_up.
The knot multiplicities and knots in the u, v and w parameter directions are then given by the function calls:
default_b_spline_knot_mult(SELF\b_spline_volume.u_degree, ku_up, uniform_knots)
default_b_spline_knots(SELF\b_spline_volume.u_degree,ku_up, uniform_knots)
default_b_spline_knot_mult(SELF\b_spline_volume.v_degree, kv_up, uniform_knots)
default_b_spline_knots(SELF\b_spline_volume.v_degree,kv_up, uniform_knots)
default_b_spline_knot_mult(SELF\b_spline_volume.w_degree, kw_up, uniform_knots)
default_b_spline_knots(SELF\b_spline_volume.w_degree,kw_up, uniform_knots)
EXPRESS specification:
*)
ENTITY uniform_volume
SUBTYPE OF (b_spline_volume);
END_ENTITY;
(*

A quasi_uniform_volume is a type of b_spline_volume in which the knots are evenly spaced, and except for the first and last, have multiplicity 1. Suitable default values for the knots and knot multiplicities are derived in this case.
A B-spline is quasi-uniform if and only if the knots are of multiplicity (degree+1) at the ends, of multiplicity 1 elsewhere, and they differ by a positive constant from the preceding knot. In this subtype the knot spacing is 1.0, starting from 0.0.
NOTE If explicit knot values for the volume are required, they can be derived as follows:
ku_up := SELF\backslash b_spline_volume.u_upper - SELF\backslash b_spline_volume.u_degree + 2
kv_up := SELF\backslash b_spline_volume.u_upper - SELF\backslash b_spline_volume.v_degree + 2
kw_up := SELF\backslash b_spline_volume.u_upper - SELF\backslash b_spline_volume.w_degree + 2
ku_up is the value required for the upper index on the knot and knot multiplicity lists in the u direction. This is computed from the degree and the number of control values in this direction.
Similar computations are used to determine kv_up, kw_up.
The knot multiplicities and knots in the u, v and w parameter directions are then given by the function calls:
default_b_spline_knot_mult(SELF\b_spline_volume.u_degree, ku_up, quasi_uniform_knots)
default_b_spline_knots(SELF\b_spline_volume.u_degree,ku_up, quasi_uniform_knots)
default_b_spline_knot_mult(SELF\b_spline_volume.v_degree, kv_up, quasi_uniform_knots)
default_b_spline_knots(SELF\b_spline_volume.v_degree,kv_up, quasi_uniform_knots)
default_b_spline_knot_mult(SELF\b_spline_volume.w_degree, kw_up, quasi_uniform_knots)
default_b_spline_knots(SELF\b_spline_volume.w_degree,kw_up, quasi_uniform_knots)
EXPRESS specification:
*)
ENTITY quasi_uniform_volume
SUBTYPE OF (b_spline_volume);
END_ENTITY;
(*

A rational_b_spline_volume is a type of b_spline_volume that is a piecewise parametric rational volume described in terms of control points, associated weight values and basis functions. It is instantiated with any of the other subtypes of b_spline_volume, which provide explicit or implicit knot values from which the basis functions are defined.
The volume is to be interpreted as follows:
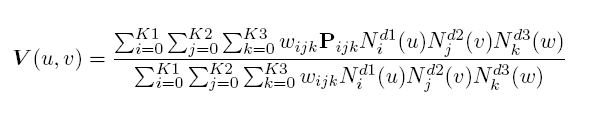
NOTE See b_spline_volume for details of the symbology used in the above equation.
EXPRESS specification:
*)
ENTITY rational_b_spline_volume
SUBTYPE OF (b_spline_volume);
weights_data : LIST[2:?] OF LIST[2:?] OF LIST[2:?] OF REAL;
DERIVE
weights : ARRAY[0:u_upper] OF ARRAY[0:v_upper] OF ARRAY[0:w_upper] OF REAL := make_array_of_array_of_array (weights_data,0,u_upper,0,v_upper,0,w_upper);
WHERE
WR1: (SIZEOF(weights_data) = SIZEOF(SELF\b_spline_volume.control_points_list)) AND (SIZEOF(weights_data[1]) = SIZEOF(SELF\b_spline_volume.control_points_list[1]))
AND (SIZEOF(weights_data[1][1]) = SIZEOF(SELF\b_spline_volume.control_points_list[1][1]));
WR2: volume_weights_positive(SELF);
END_ENTITY;
(*
Attribute definitions:
weights_data: the weights associated with the control points in the rational case;
weights: the array (three-dimensional) of weight values constructed from the weights_data.
Formal propositions:
WR1: The array dimensions for the weights shall be consistent with the control points data.
WR2: The weight value associated with each control point shall be greater than zero.

A locally_refined_spline_volume is a type of volume that is a piecewise parametric polynomial or rational volume described in terms of control points and local B-spline functions. If the set of B-spline functions are linearly independent, they will form a basis. With appropriate attribute values, the volume is capable of representing single span or spline volumes of explicit polynomial, rational, Bézier or B-spline type. However, the locally_ refined_spline_volume entity is intended for spline volumes that do not have a tensor product structure. The degree of the volume can vary as the B-splines from which it is defined, need not to have the same polynomial degree.
NOTE 1 A locally refined spline volume is rational if and only if the weights are not all identical; this can be represented by the rational_locally_refined_spline_volume subtype. If it is polynomial, the weights may be defaulted to all being 1.
The entity locally_refined_spline_volume can, with proper pre and post processing, be used to represent volumes of the types:
Interpretation of the data is as follows:
The volume, in the polynomial case, is given by:
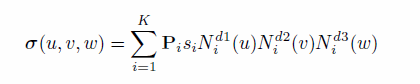
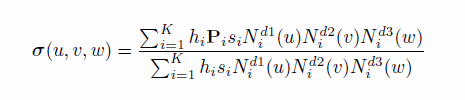
K = number of control points,
P i = control points(i),
si = scaling_factors(i),
hi = weights_data(i),
N i d1(u) = u_bspline(i), and
d1=u_degree.
N i d2(v) = v_bspline(i), and
d2=v_degree.
N i d3(w) = v_bspline(i), and
d3=v_degree.
NOTE 2 Scaling factors are necessary to ensure that the non-zero B-spline basis functions add up to unity (partition of unity) at all points in the domain of semi_standard_t_spline and lr_b_spline definitions. For analysis_suitable_t_spline, standard_t_spline, and hierarchical_b_spline, the scaling factor is always equal to 1.0. The collection of B-spline basis functions for analysis_suitable_t_spline and standard_t_spline definitions form a partition of unity, while for hierarchical_b_spline there is no partition of unity achieved.
NOTE 3 The degrees are associated with the local_b_splines and do not need to be constant throughout the volume.
The weights, in the case of the rational subtype, are given in the same sequence as the coefficients. The knot values and multiplicities are defined in the entity local_b_spline. The B-splines are defined over a domain described by knot vectors in the parameter directions of the volume. However, in contrast to B-bspline volumes, the basis functions or B-splines do not need to adapt to all knot lines in their supports. This facilitates the definition of a spline volume on a box partition.
NOTE 4 When the polynomial degree is the same for all B-splines and no knot lines exist that do not cross the entire parameter domain, the locally_refined_spline_volume will coincide with b_spline_volume_with_knots. In that case b_spline_volume_with_knots has the simplest and most compact representation.
NOTE 5 A locally_refined_spline_volume can be of type analysis suitable T-spline, hierarchical B-spline, LR-spline, semi standard T-spline or standard T-spline. The type is given by the enumeration locally_refined_spline_type_enum, and the packing and unpacking of the volume will depend on this type.
EXPRESS specification:
*)
ENTITY locally_refined_spline_volume
SUBTYPE OF (volume);
u_b_splines : LIST[8:?] OF local_b_spline;
v_b_splines : LIST[8:?] OF local_b_spline;
w_b_splines : LIST[8:?] OF local_b_spline;
u_knots : spline_knot_values;
v_knots : spline_knot_values;
w_knots : spline_knot_values;
control_points_list : LIST[8:?] OF cartesian_point;
scaling_factors : LIST[8:?] OF REAL;
linearly_independent : linearly_independent_enum;
locally_refined_spline_type : locally_refined_spline_type_enum;
domain : LIST[3:3] OF LIST[2:2] OF REAL;
WHERE
WR1: SIZEOF(u_b_splines) = SIZEOF(control_points_list);
WR2: SIZEOF(v_b_splines) = SIZEOF(control_points_list);
WR3: SIZEOF(w_b_splines) = SIZEOF(control_points_list);
WR4: SIZEOF(scaling_factors) = SIZEOF(control_points_list);
WR5: constraints_scaling(scaling_factors);
END_ENTITY;
(*
Attribute definitions:
u_b_splines: the local_b_spline functions in the first (u) parameter direction from which the volume is defined. These functions refer to the u_knots list for their knot parameter values.
v_b_splines: the local_b_spline functions in the second (v) parameter direction from which the volume is defined. These functions refer to the v_knots list for their knot parameter values.
w_b_splines: the local_b_spline functions in the thirdd (w) parameter direction from which the volume is defined. These functions refer to the w_knots list for their knot parameter values.
NOTE 6 There may be some repetitions in the 3 lists of local_b_splines.
u_knots: the list of knot values for parameter u;
v_knots: the list of knot values for parameter v;
w_knots: the list of knot values for parameter w;
control_points_list: the list of control points. The control_points_list and consequently also the u_b_splines, the v_b_splines, the w_b_splines and scaling_factors, are ordered according to the knot values of the the combined B-spline coefficient constructed by multiplying corresponding univariate B-splines, starting from the lowest knot value for each parameter. The knots in the w-parameter are the major sorting factor followed by knots in the v direction and finally the u direction. In case of ambiguities, the lists are sorted according to the maximum knot values of the combined B-splines and the multiplicities of the first knots of the univariate B-splines.
scaling_factors: the list of scaling factors used to ensure that the non-zero B-spline basis functions add up to unity (partition of unity) at all points in the domain. Scaling factors not equal to 1.0 are sometimes needed for semi_standard_t_spline and lr_b_spline definitions to ensure that the collection of B-spline basis functions form a partition of unity. For analysis_suitable_t_spline and standard_t_spline definitions, partition of unity is achieved without use of scaling factors (i.e., the scaling factor is always equal to 1.0). For hierarchical_b_spline definitions, a scaling factor equal to 1.0 is used, although there is no partition of unity achieved.
linearly_independent: indicates whether this property has been tested for and in that case the result of the test; this is for information only;
NOTE 7 The test is applied to the set of products of local_b_splines used as coefficients of the control points . Not all types of locally refined volumes are linearly independent by default.
locally_refined_spline_type: the type of the initial locally refined spline volume that provides rules for how the stored volume can be unpacked to its original format;
domain: the parameter domain corresponding to the volume. domain(1),(1) and domain (1),(2) give the minimum and maximum parameter values in the u direction; domain(2),(1) and domain (2),(2) give the minimum and maximum parameter values in the v direction; domain(3),(1) and domain (3),(2) give the minimum and maximum parameter values in the w direction. If all B-splines at the boundary have a knot multiplicity equal to the degree+1 at this boundary, the domain will coincide with the domain given by the minimum and maximum values in u_knots , v_knots and w_knots. Otherwise, it will be coincide with a domain given by nearby knots depending on knot multiplicities.
Formal propositions:
WR1: the number of u_b_splines shall be equal to the number of control points;
WR2: the number of v_b_splines shall be equal to the number of control points
WR3: the number of w_b_splines shall be equal to the number of control points;
WR4: the number of scaling_factors shall be equal to the number of control points;
WR5: all scaling_factors shall be positive and not greater than 1.0.

A rational_locally_refined_spline_volume is a type of locally_refined_spline_volume that is a piecewise parametric rational volume described in terms of control points and local B-spline functions.
EXPRESS specification:
*)
ENTITY rational_locally_refined_spline_volume
SUBTYPE OF (locally_refined_spline_volume);
weights_data : LIST[8:?] OF REAL;
WHERE
WR1: SIZEOF(weights_data) = SIZEOF(SELF\locally_refined_spline_volume.control_points_list);
WR2: weights_positive(weights_data);
END_ENTITY;
(*
Attribute definitions:
weights_data: the supplied values of the weights.
Formal propositions:
WR1: the size of the of weights_data list shall be equal to the number of control points
WR2: all values in the weights_data list shall be positive.
EXPRESS specification:
*)
FUNCTION above_plane (p1 : cartesian_point; p2 : cartesian_point; p3 : cartesian_point; p4 : cartesian_point) : REAL;
LOCAL
dir2, dir3, dir4 : direction :=
dummy_gri || direction([1.0, 0.0, 0.0]);
val, mag : REAL;
END_LOCAL;
IF (p1.dim <> 3) THEN
RETURN(?);
END_IF;
REPEAT i := 1 TO 3;
dir2.direction_ratios[i] := p2.coordinates[i] - p1.coordinates[i];
dir3.direction_ratios[i] := p3.coordinates[i] - p1.coordinates[i];
dir4.direction_ratios[i] := p4.coordinates[i] - p1.coordinates[i];
mag := dir4.direction_ratios[i]*dir4.direction_ratios[i];
END_REPEAT;
mag := sqrt(mag);
val := mag*dot_product(dir4, cross_product(dir2, dir3).orientation);
RETURN(val);
END_FUNCTION;
(*
Argument definitions:
p1: (input) the first cartesian_point to be tested as a member of a coplanar set;
p2: the second cartesian_point to be tested as a member of a coplanar set;
p3: (input) the third cartesian_point to be tested as a member of a coplanar set;
p4: the fourth cartesian_point to be tested as a member of a coplanar set;
EXPRESS specification:
*)
FUNCTION acyclic_curve_replica (rep : curve_replica; parent : curve) : BOOLEAN;
IF NOT (('GEOMETRY_SCHEMA.CURVE_REPLICA') IN TYPEOF(parent)) THEN
RETURN (TRUE);
END_IF;
(* Return TRUE if the parent is not of type curve_replica *)
IF (parent :=: rep) THEN
RETURN (FALSE);
(* Return FALSE if the parent is the same curve_replica, otherwise,
call function again with the parents own parent_curve. *)
ELSE
RETURN(acyclic_curve_replica(rep,
parent\curve_replica.parent_curve));
END_IF;
END_FUNCTION;
(*
Argument definitions:
rep: (input) The curve_replica which is to be tested for a cyclic reference.
parent: a curve used in the definition of the replica.
EXPRESS specification:
*)
FUNCTION acyclic_point_replica (rep : point_replica; parent : point) : BOOLEAN;
IF NOT (('GEOMETRY_SCHEMA.POINT_REPLICA') IN TYPEOF(parent)) THEN
RETURN (TRUE);
END_IF;
(* Return TRUE if the parent is not of type point_replica *)
IF (parent :=: rep) THEN
RETURN (FALSE);
(* Return FALSE if the parent is the same point_replica, otherwise,
call function again with the parents own parent_pt. *)
ELSE RETURN(acyclic_point_replica(rep, parent\point_replica.parent_pt));
END_IF;
END_FUNCTION;
(*
Argument definitions:
rep: (input) the point_replica which is to be tested for acyclic reference;
parent: (input) the point used to define the replica.
EXPRESS specification:
*)
FUNCTION acyclic_surface_replica (rep : surface_replica; parent : surface) : BOOLEAN;
IF NOT (('GEOMETRY_SCHEMA.SURFACE_REPLICA') IN TYPEOF(parent)) THEN
RETURN (TRUE);
END_IF;
(* Return TRUE if the parent is not of type surface_replica *)
IF (parent :=: rep) THEN
RETURN (FALSE);
(* Return FALSE if the parent is the same surface_replica, otherwise,
call function again with the parents own parent_surface. *)
ELSE RETURN(acyclic_surface_replica(rep,
parent\surface_replica.parent_surface));
END_IF;
END_FUNCTION;
(*
Argument definitions:
rep: (input) The surface_replica which is to be tested for acyclic reference.
parent: (input) A surface used in the definition of the replica.
EXPRESS specification:
*)
FUNCTION associated_surface (arg : pcurve_or_surface) : surface;
LOCAL
surf : surface;
END_LOCAL;
IF 'GEOMETRY_SCHEMA.PCURVE' IN TYPEOF(arg) THEN
surf := arg\pcurve.basis_surface;
ELSE
surf := arg;
END_IF;
RETURN(surf);
END_FUNCTION;
(*
Argument definitions:
arg: (input) The pcurve_or_surface for which the determination of the associated parent surface is required.
The base_axis function returns normalised orthogonal directions, u[1], u[2] and, if appropriate, u[3].
In the three-dimensional case, with complete input data, u[3] is in the direction of axis3, u[1] is in the direction of the projection of axis1 onto the plane normal to u[3], and u[2] is orthogonal to both u[1] and u[3], taking the same sense as axis2.
In the two-dimensional case u[1] is in the direction of axis1 and u[2] is perpendicular to this, taking its sense from axis2.
For incomplete input data appropriate default values are derived.
NOTE This function does not provide geometric founding for the directions returned, the caller of the the function is responsible for ensuring that they are used in a representation with a geometric_representation_context.
EXPRESS specification:
*)
FUNCTION base_axis (dim : INTEGER; axis1 : direction; axis2 : direction; axis3 : direction) : LIST[2:3] OF direction;
LOCAL
u : LIST [2:3] OF direction;
factor : REAL;
d1, d2 : direction;
END_LOCAL;
IF (dim = 3) THEN
d1 := NVL(normalise(axis3), dummy_gri || direction([0.0,0.0,1.0]));
d2 := first_proj_axis(d1,axis1);
u := [d2, second_proj_axis(d1,d2,axis2), d1];
ELSE
IF EXISTS(axis1) THEN
d1 := normalise(axis1);
u := [d1, orthogonal_complement(d1)];
IF EXISTS(axis2) THEN
factor := dot_product(axis2,u[2]);
IF (factor < 0.0) THEN
u[2].direction_ratios[1] := -u[2].direction_ratios[1];
u[2].direction_ratios[2] := -u[2].direction_ratios[2];
END_IF;
END_IF;
ELSE
IF EXISTS(axis2) THEN
d1 := normalise(axis2);
u := [orthogonal_complement(d1), d1];
u[1].direction_ratios[1] := -u[1].direction_ratios[1];
u[1].direction_ratios[2] := -u[1].direction_ratios[2];
ELSE
u := [dummy_gri || direction([1.0, 0.0]), dummy_gri ||
direction([0.0, 1.0])];
END_IF;
END_IF;
END_IF;
RETURN(u);
END_FUNCTION;
(*
Argument definitions:
dim: (input) The integer value of the dimensionality of the space in which the normalised orthogonal directions are required.
axis1: (input) A direction used as a first approximation to the direction of output axis u[1].
axis2: (input) A direction used to determine the sense of u[2].
axis3: (input) The direction of u[3] in the case dim = 3, or indeterminate in the case dim = 2.
The build_2axes function returns two normalised orthogonal directions. u[1] is in the direction of
ref_direction and u[2] is perpendicular to u[1].
A default value of (1.0, 0.0) is supplied for ref_direction if the input data is incomplete.
NOTE This function does not provide geometric founding for the directions returned, the caller of the the function is responsible for ensuring that they are used in a representation with a geometric_representation_context.
EXPRESS specification:
*)
FUNCTION build_2axes (ref_direction : direction) : LIST[2:2] OF direction;
LOCAL
d : direction := NVL(normalise(ref_direction),
dummy_gri || direction([1.0,0.0]));
END_LOCAL;
RETURN([d, orthogonal_complement(d)]);
END_FUNCTION;
(*
Argument definitions:
ref_direction: (input) A reference direction in 2 dimensional space, this may be defaulted to (1.0, 0.0).
The build_axes function returns three normalised orthogonal directions. u[3] is in the direction of axis, u[1] is in the direction of the projection of ref_direction onto the plane normal to u[3], and u[2] is the cross product of u[3] and u[1]. Default values are supplied if input data is incomplete.
NOTE This function does not provide geometric founding for the directions returned, the caller of the the function is responsible for ensuring that they are used in a representation with a geometric_representation_context.
EXPRESS specification:
*)
FUNCTION build_axes (axis : direction; ref_direction : direction) : LIST[3:3] OF direction;
LOCAL
d1, d2 : direction;
END_LOCAL;
d1 := NVL(normalise(axis), dummy_gri || direction([0.0,0.0,1.0]));
d2 := first_proj_axis(d1, ref_direction);
RETURN([d2, normalise(cross_product(d1,d2))\vector.orientation, d1]);
END_FUNCTION;
(*
Argument definitions:
axis: (input) The intended direction of u[3], this may be defaulted to (0.0, 0.0, 1.0).
ref_direction: (input) A direction in a direction used to compute u[1].
The check_geometric_dimension function checks that whenever a cartesian_point.is used in a representation the number of coordinates is equal to the dimensionality of the corresponding geometric_representation_context. The function also checkes that whenever a direction is used in a representation the number of direction ratios is equal to the dimensionality of the corresponding geometric_representation_context.
The function first determines whether there are mixed dimensions in the contexts, if not a simple check of the numbers of coordinates or direction ratios is sufficient. In other cases each point or direction is checked against the dimensionalites of all the contexts in which it is used. The value FALE is returned if any mis-match of dimensions is detected.
EXPRESS specification:
*)
FUNCTION check_geometric_dimension (capt : SET[0:?] OF cartesian_point; dir : SET[0:?] OF direction; grc : SET[1:?] OF geometric_representation_context) : BOOLEAN;
LOCAL
globaldim : INTEGER := 0; (* means mixed dimensionality *)
reps : SET [0:?] OF representation := [];
result : BOOLEAN := TRUE; (* means no error *)
END_LOCAL;
globaldim:= geometric_dimensionalities_in_contexts(grc);
IF (globaldim > 0) then
(* Same dimension for all contexts; only one check needed. *)
IF (SIZEOF(capt) > 0) THEN
REPEAT i := 1 TO HIINDEX(capt);
IF (HIINDEX(capt[i].coordinates) <> globaldim) THEN
RETURN(FALSE);
END_IF;
END_REPEAT;
END_IF;
IF (SIZEOF(dir) > 0) THEN
REPEAT i := 1 TO HIINDEX(dir);
IF (HIINDEX(dir[i].direction_ratios) <> globaldim) THEN
RETURN(FALSE);
END_IF;
END_REPEAT;
END_IF;
RETURN(result);
ELSE
(* globaldim=0, mixed dimensions for contexts; check needed for context of each representation in which gri is used. *)
IF (SIZEOF(capt) > 0) THEN
REPEAT i := 1 TO HIINDEX(capt);
reps := using_representations(capt[i]);
IF (SIZEOF(reps) > 0) THEN
REPEAT j := 1 TO HIINDEX(reps);
IF (HIINDEX(capt[i].coordinates) <> reps[j].context_of_items\geometric_representation_context.coordinate_space_dimension) THEN
RETURN(FALSE);
END_IF;
END_REPEAT;
ELSE (* zero reps *)
RETURN(FALSE);
END_IF;
END_REPEAT;
END_IF;
IF (SIZEOF(dir) > 0) THEN
REPEAT i := 1 TO HIINDEX(dir);
(* globaldim=0, Mixed dimensions for contexts, check needed for context of each representation in which gri is used *)
reps := using_representations(dir[i]);
IF (SIZEOF(reps) > 0) THEN
REPEAT j := 1 TO HIINDEX(reps);
IF (HIINDEX(dir[i].direction_ratios) <> reps[j].context_of_items\geometric_representation_context.coordinate_space_dimension) THEN
RETURN(FALSE);
END_IF;
END_REPEAT;
ELSE (* zero reps *)
RETURN(FALSE);
END_IF;
END_REPEAT;
END_IF;
END_IF;
RETURN(result);
END_FUNCTION;
(*
Argument definitions:
capt: (input) A set of cartesian_points to be checked against context dimensionalities.
dir: (input) A set of directions to be checked against context dimensionalities.
grc: (input) The set of geometric_representation_contexts in which the points or directions might be used.
EXPRESS specification:
*)
FUNCTION constraints_composite_curve_on_surface (c : composite_curve_on_surface) : BOOLEAN;
LOCAL
n_segments : INTEGER := SIZEOF(c.segments);
END_LOCAL;
REPEAT k := 1 TO n_segments;
IF (NOT('GEOMETRY_SCHEMA.PCURVE' IN
TYPEOF(c\composite_curve.segments[k].parent_curve))) AND
(NOT('GEOMETRY_SCHEMA.SURFACE_CURVE' IN
TYPEOF(c\composite_curve.segments[k].parent_curve))) AND
(NOT('GEOMETRY_SCHEMA.COMPOSITE_CURVE_ON_SURFACE' IN
TYPEOF(c\composite_curve.segments[k].parent_curve))) THEN
RETURN (FALSE);
END_IF;
END_REPEAT;
RETURN(TRUE);
END_FUNCTION;
(*
Argument definitions:
c: (input) A composite_curve_on_surface to be verified.
The constraints_param_b_spline function checks the parametrisation of a B-spline curve or (one of the directions of) a B-spline surface or volume and returns TRUE if no inconsistencies are found.
These constraints are:
Degree ≥ 1.
Upper index on knots ≥ 2.
Upper index on control points ≥ degree.
Sum of knot multiplicities = degree + (upper index on control points) + 2.
For the first and last knot the multiplicity is bounded by 1 and (degree+1).
For all other knots the knot multiplicity is bounded by 1 and degree.
The consecutive knots are increasing in value.
EXPRESS specification:
*)
FUNCTION constraints_param_b_spline (degree : INTEGER; up_knots : INTEGER; up_cp : INTEGER; knot_mult : LIST[0:?] OF INTEGER; knots : LIST[0:?] OF parameter_value) : BOOLEAN;
LOCAL
result : BOOLEAN := TRUE;
k, sum : INTEGER;
END_LOCAL;
(* Find sum of knot multiplicities. *)
sum := knot_mult[1];
REPEAT i := 2 TO up_knots;
sum := sum + knot_mult[i];
END_REPEAT;
(* Check limits holding for all B-spline parametrisations *)
IF (degree < 1) OR (up_knots < 2) OR (up_cp < degree) OR
(sum <> (degree + up_cp + 2)) THEN
result := FALSE;
RETURN(result);
END_IF;
k := knot_mult[1];
IF (k < 1) OR (k > degree + 1) THEN
result := FALSE;
RETURN(result);
END_IF;
REPEAT i := 2 TO up_knots;
IF (knot_mult[i] < 1) OR (knots[i] <= knots[i-1]) THEN
result := FALSE;
RETURN(result);
END_IF;
k := knot_mult[i];
IF (i < up_knots) AND (k > degree) THEN
result := FALSE;
RETURN(result);
END_IF;
IF (i = up_knots) AND (k > degree + 1) THEN
result := FALSE;
RETURN(result);
END_IF;
END_REPEAT;
RETURN(result);
END_FUNCTION;
(*
Argument definitions:
degree: (input) an integer defining the degree of the B-spline basis functions.
up_knots: (input) an integer giving the upper index of the list of knot multiplicities.
up_cp: ((input) an integer which is the upper index of the control points for the curve or surface being checked for consistency of its parameter values;
knot_mult: (input) the list of knot multiplicities;
knots: (input) the list of knot values to be checked.
The constraints_param_local_b_spline function checks the parameters defining a local_b_spline and returns TRUE if no inconsistencies are found. These constraints are:
These constraints are:
Degree ≥= 1.
Upper index on knots ≥= 2.
Sum of knot multiplicities = degree + 2.
For the first and last knot the multiplicity is bounded by 1 and (degree+1).
For all other knots the knot multiplicity is bounded by 1 and degree.
The first knot pointer is at least 1 and consecutive knot pointers are increasing in value.
EXPRESS specification:
*)
FUNCTION constraints_param_local_b_spline (degree : INTEGER; knot_mult : LIST[0:?] OF INTEGER; knots : LIST[0:?] OF INTEGER) : BOOLEAN;
LOCAL result : BOOLEAN := TRUE; k, up_knots, sum : INTEGER; END_LOCAL; (* Find sum of knot multiplicities. *) up_knots := SIZEOF(knots); sum := knot_mult[1]; REPEAT i := 2 TO up_knots; sum := sum + knot_mult[i]; END_REPEAT; (* Check limits holding for all B-spline parametrisations *) IF (degree < 1) OR (up_knots < 2) OR (sum <> (degree + 2)) THEN result := FALSE; RETURN(result); END_IF; k := knot_mult[1]; IF (k < 1) OR (k > degree + 1) THEN result := FALSE; RETURN(result); END_IF; (* first pointer shall be 1 or more *) IF (knots[1] < 1) THEN result := FALSE; END_IF; REPEAT i := 2 TO up_knots; IF (knot_mult[i] < 1) OR (knots[i] <= knots[i-1]) THEN result := FALSE; RETURN(result); END_IF; k := knot_mult[i]; IF (i < up_knots) AND (k > degree) THEN result := FALSE; RETURN(result); END_IF; IF (i = up_knots) AND (k > degree + 1) THEN result := FALSE; RETURN(result); END_IF; END_REPEAT; RETURN(result);
END_FUNCTION;
(*
Argument definitions:
degree: (input) an integer defining the degree of the B-spline basis functions.
knot_mult: (input) the list of knot multiplicities;
knots: (input) the list of integer pointers to the knot values.
The constraints_rectangular_composite_surface functions checks the following constraints on the attributes of a rectangular composite surface:
that the component surfaces are all either rectangular trimmed surfaces or B-spline surfaces;
that the transition attributes of the segments array do not contain the value discontinuous except for the last row or column, where they indicate that the surface is not closed in the appropriate direction.
EXPRESS specification:
*)
FUNCTION constraints_rectangular_composite_surface (s : rectangular_composite_surface) : BOOLEAN;
REPEAT i := 1 TO s.n_u;
REPEAT j := 1 TO s.n_v;
IF NOT (('GEOMETRY_SCHEMA.B_SPLINE_SURFACE' IN TYPEOF
(s.segments[i][j].parent_surface)) OR
('GEOMETRY_SCHEMA.RECTANGULAR_TRIMMED_SURFACE' IN TYPEOF
(s.segments[i][j].parent_surface))) THEN
RETURN(FALSE);
END_IF;
END_REPEAT;
END_REPEAT;
(* Check the transition codes, omitting the last row or column *)
REPEAT i := 1 TO s.n_u-1;
REPEAT j := 1 TO s.n_v;
IF s.segments[i][j].u_transition = discontinuous THEN
RETURN(FALSE);
END_IF;
END_REPEAT;
END_REPEAT;
REPEAT i := 1 TO s.n_u;
REPEAT j := 1 TO s.n_v-1;
IF s.segments[i][j].v_transition = discontinuous THEN
RETURN(FALSE);
END_IF;
END_REPEAT;
END_REPEAT;
RETURN(TRUE);
END_FUNCTION;
(*
Argument definitions:
s: (input) A rectangular composite surface to be verified.
The constraints_scaling function checks the scaling factors associated with the control points of a locally refined curve, surface or volume and returns TRUE if they are all positive and less than 1.0.
EXPRESS specification:
*)
FUNCTION constraints_scaling (factors : LIST[0:?] OF REAL) : BOOLEAN;
LOCAL
result : BOOLEAN := TRUE;
END_LOCAL;
REPEAT i := 1 TO SIZEOF(factors);
IF NOT({0.0 < factors[i] <= 1.0}) THEN
result := FALSE;
RETURN(result);
END_IF;
END_REPEAT;
RETURN(result);
END_FUNCTION;
(*
Argument definitions:
factors: (input) a LIST of scaling factor values to be tested.
NOTE This function does not provide geometric founding for the vector returned, the caller of the the function is responsible for ensuring that it is used in a representation with a geometric_representation_context.
EXPRESS specification:
*)
FUNCTION cross_product (arg1 : direction; arg2 : direction) : vector;
LOCAL
mag : REAL;
res : direction;
v1,v2 : LIST[3:3] OF REAL;
result : vector;
END_LOCAL;
IF ( NOT EXISTS (arg1) OR (arg1.dim = 2)) OR
( NOT EXISTS (arg2) OR (arg2.dim = 2)) THEN
RETURN(?);
ELSE
BEGIN
v1 := normalise(arg1).direction_ratios;
v2 := normalise(arg2).direction_ratios;
res := dummy_gri || direction([(v1[2]*v2[3] - v1[3]*v2[2]),
(v1[3]*v2[1] - v1[1]*v2[3]), (v1[1]*v2[2] - v1[2]*v2[1])]);
mag := 0.0;
REPEAT i := 1 TO 3;
mag := mag + res.direction_ratios[i]*res.direction_ratios[i];
END_REPEAT;
IF (mag > 0.0) THEN
result := dummy_gri || vector(res, SQRT(mag));
ELSE
result := dummy_gri || vector(arg1, 0.0);
END_IF;
RETURN(result);
END;
END_IF;
END_FUNCTION;
(*
Argument definitions:
arg1: (input) a direction defining the first operand in cross product operation.
arg2: (input) a direction defining the second operand for cross product.
EXPRESS specification:
*)
FUNCTION curve_weights_positive (b : rational_b_spline_curve) : BOOLEAN;
LOCAL
result : BOOLEAN := TRUE;
END_LOCAL;
REPEAT i := 0 TO b.upper_index_on_control_points;
IF b.weights[i] <= 0.0 THEN
result := FALSE;
RETURN(result);
END_IF;
END_REPEAT;
RETURN(result);
END_FUNCTION;
(*
Argument definitions:
b: (input) a rational B-spline curve for which the weight values are to be tested.
EXPRESS specification:
*)
FUNCTION default_b_spline_curve_weights (up_cp : INTEGER) : ARRAY[0:up_cp] OF REAL;
RETURN([1:up_cp + 1]);
END_FUNCTION;
(*
Argument definitions:
up_cp: (input) an integer defining the upper index on the array of the B-spline curve weights required.
EXPRESS specification:
*)
FUNCTION default_b_spline_knot_mult (degree : INTEGER; up_knots : INTEGER; uniform : knot_type) : LIST[2:?] OF INTEGER;
LOCAL
knot_mult : LIST [1:up_knots] OF INTEGER;
END_LOCAL;
IF uniform = uniform_knots THEN
knot_mult := [1:up_knots];
ELSE
IF uniform = quasi_uniform_knots THEN
knot_mult := [1:up_knots];
knot_mult[1] := degree + 1;
knot_mult[up_knots] := degree + 1;
ELSE
IF uniform = piecewise_bezier_knots THEN
knot_mult := [degree:up_knots];
knot_mult[1] := degree + 1;
knot_mult[up_knots] := degree + 1;
ELSE
knot_mult := [0:up_knots];
END_IF;
END_IF;
END_IF;
RETURN(knot_mult);
END_FUNCTION;
(*
Argument definitions:
degree: (input) an integer defining the degree of the B-spline basis functions.
up_knots: (input) an integer which gives the number of knot multiplicities required.
uniform: (input) the type of basis function for which knot multiplicities are required.
EXPRESS specification:
*)
FUNCTION default_b_spline_knots (degree : INTEGER; up_knots : INTEGER; uniform : knot_type) : LIST[2:?] OF parameter_value;
LOCAL
knots : LIST [1:up_knots] OF parameter_value := [0:up_knots];
ishift : INTEGER := 1;
END_LOCAL;
IF (uniform = uniform_knots) THEN
ishift := degree + 1;
END_if;
IF (uniform = uniform_knots) OR
(uniform = quasi_uniform_knots) OR
(uniform = piecewise_bezier_knots) THEN
REPEAT i := 1 TO up_knots;
knots[i] := i - ishift;
END_REPEAT;
END_IF;
RETURN(knots);
END_FUNCTION;
(*
Argument definitions:
degree: (input) an integer defining the degree of the B-spline basis functions.
up_knots: (input) an integer which gives the number of knot values required.
uniform: (input) the type of basis function for which knots are required.
EXPRESS specification:
*)
FUNCTION default_b_spline_surface_weights (u_upper : INTEGER; v_upper : INTEGER) : ARRAY[0:u_upper] OF ARRAY[0:v_upper] OF REAL;
RETURN([[1:v_upper + 1]:u_upper +1]);
END_FUNCTION;
(*
Argument definitions:
u_upper: (input) an integer defining the upper index on the array of the B-spline surface weights required in the u direction.
v_upper: (input) an integer defining the upper index on the array of the B-spline surface weights required in the v direction.
EXPRESS specification:
*)
FUNCTION dimension_of (item : geometric_representation_item) : dimension_count;
LOCAL
x : SET OF representation;
y : representation_context;
dim : dimension_count;
END_LOCAL;
-- For cartesian_point, direction, or vector dimension is determined by
-- counting components.
IF 'GEOMETRY_SCHEMA.CARTESIAN_POINT' IN TYPEOF(item) THEN
dim := SIZEOF(item\cartesian_point.coordinates);
RETURN(dim);
END_IF;
IF 'GEOMETRY_SCHEMA.DIRECTION' IN TYPEOF(item) THEN
dim := SIZEOF(item\direction.direction_ratios);
RETURN(dim);
END_IF;
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF(item) THEN
dim := SIZEOF(item\vector.orientation\direction.direction_ratios);
RETURN(dim);
END_IF;
-- For all other types of geometric_representation_item dim is obtained
-- via context.
-- Find the set of representation in which the item is used.
x := using_representations(item);
-- Determines the dimension_count of the
-- geometric_representation_context.
-- The SET x is non-empty for legal instances since this is required by WR1 of
-- representation_item.
IF (SIZEOF(x) > 0) THEN
y := x[1].context_of_items;
dim := y\geometric_representation_context.coordinate_space_dimension;
RETURN (dim);
ELSE
RETURN(?);
-- mark error by returning indeterminate result
END_IF;
END_FUNCTION;
(*
Argument definitions:
item: (input) a geometric_representation_item for which the dimension_count is determined.
EXPRESS specification:
*)
FUNCTION dot_product (arg1 : direction; arg2 : direction) : REAL;
LOCAL
scalar : REAL;
vec1, vec2: direction;
ndim : INTEGER;
END_LOCAL;
IF NOT EXISTS (arg1) OR NOT EXISTS (arg2) THEN
scalar := ?;
(* When function is called with invalid data an indeterminate result
is returned *)
ELSE
IF (arg1.dim <> arg2.dim) THEN
scalar := ?;
(* When function is called with invalid data an indeterminate result
is returned *)
ELSE
BEGIN
vec1 := normalise(arg1);
vec2 := normalise(arg2);
ndim := arg1.dim;
scalar := 0.0;
REPEAT i := 1 TO ndim;
scalar := scalar +
vec1.direction_ratios[i]*vec2.direction_ratios[i];
END_REPEAT;
END;
END_IF;
END_IF;
RETURN (scalar);
END_FUNCTION;
(*
Argument definitions:
arg1: (input)a direction defining first vector in dot product, or scalar product, operation..
arg2: (input) a direction defining second operand for dot product operation.
NOTE This function does not provide geometric founding for the direction returned, the caller of the the function is responsible for ensuring that it is used in a representation with a geometric_representation_context.
EXPRESS specification:
*)
FUNCTION first_proj_axis (z_axis : direction; arg : direction) : direction;
LOCAL
x_axis : direction;
v : direction;
z : direction;
x_vec : vector;
END_LOCAL;
IF (NOT EXISTS(z_axis)) THEN
RETURN (?) ;
ELSE
z := normalise(z_axis);
IF NOT EXISTS(arg) THEN
IF ((z.direction_ratios <> [1.0,0.0,0.0]) AND
(z.direction_ratios <> [-1.0,0.0,0.0])) THEN
v := dummy_gri || direction([1.0,0.0,0.0]);
ELSE
v := dummy_gri || direction([0.0,1.0,0.0]);
END_IF;
ELSE
IF (arg.dim <> 3) THEN
RETURN (?) ;
END_IF;
IF ((cross_product(arg,z).magnitude) = 0.0) THEN
RETURN (?);
ELSE
v := normalise(arg);
END_IF;
END_IF;
x_vec := scalar_times_vector(dot_product(v, z), z);
x_axis := vector_difference(v, x_vec).orientation;
x_axis := normalise(x_axis);
END_IF;
RETURN(x_axis);
END_FUNCTION;
(*
Argument definitions:
z_axis: (input) A direction defining a local Z coordinate axis.
arg: (input) A direction not parallel to z_axis..
arg: (output) A direction which is in the direction of the projection of arg onto the plane with normal z_axis.
The geometric_dimensionalities_in_contexts function checks the different values of dimensionality which are found in a set of geometric_representation_contexts. If all contexts have the same coordinate_space_dimension then the integer value 1, 2, or 3 is returned depending upon the shared value for coordinate_space_dimension. If mixed values are found the ineger 0 is returned.
EXPRESS specification:
*)
FUNCTION geometric_dimensionalities_in_contexts (grcs : SET[1:?] OF geometric_representation_context) : INTEGER;
LOCAL
grcs_1d : INTEGER := 0;
grcs_2d : INTEGER := 0;
grcs_3d : INTEGER := 0;
END_LOCAL;
IF (SIZEOF(grcs) = 1) THEN
(* only one geometric_context, will be one type of dimension anyway *)
RETURN(grcs[1]\geometric_representation_context.coordinate_space_dimension);
ELSE
REPEAT i := 1 TO HIINDEX(grcs);
IF (grcs[i]\geometric_representation_context.coordinate_space_dimension = 1) THEN
grcs_1d := grcs_1d + 1;
ELSE
IF (grcs[i]\geometric_representation_context.coordinate_space_dimension = 2) THEN
grcs_2d := grcs_2d + 1;
ELSE
IF (grcs[i]\geometric_representation_context.coordinate_space_dimension = 3) THEN
grcs_3d := grcs_3d + 1;
END_IF;
END_IF;
END_IF;
END_REPEAT;
END_IF;
IF (grcs_1d + grcs_2d = 0) THEN
RETURN(3);
ELSE
IF (grcs_1d + grcs_3d = 0) THEN
RETURN(2);
ELSE
IF (grcs_2d + grcs_3d = 0) THEN
RETURN(1);
ELSE
RETURN(0); (* multiple dimensions *)
END_IF;
END_IF;
END_IF;
END_FUNCTION;
(*
Argument definitions:
grcs: (input) The set of geometric_representation_contexts to be checked for mixed dimensionality.
EXPRESS specification:
*)
FUNCTION get_basis_surface (c : curve_on_surface) : SET[0:2] OF surface;
LOCAL
surfs : SET[0:2] OF surface;
n : INTEGER;
END_LOCAL;
surfs := [];
IF 'GEOMETRY_SCHEMA.PCURVE' IN TYPEOF (c) THEN
surfs := [c\pcurve.basis_surface];
ELSE
IF 'GEOMETRY_SCHEMA.SURFACE_CURVE' IN TYPEOF (c) THEN
n := SIZEOF(c\surface_curve.associated_geometry);
REPEAT i := 1 TO n;
surfs := surfs +
associated_surface(c\surface_curve.associated_geometry[i]);
END_REPEAT;
END_IF;
END_IF;
IF 'GEOMETRY_SCHEMA.COMPOSITE_CURVE_ON_SURFACE' IN TYPEOF (c) THEN
(* For a composite_curve_on_surface the basis_surface is the intersection
of the basis_surfaces of all the segments. *)
n := SIZEOF(c\composite_curve.segments);
surfs := get_basis_surface(
c\composite_curve.segments[1].parent_curve);
IF n > 1 THEN
REPEAT i := 2 TO n;
surfs := surfs * get_basis_surface(
c\composite_curve.segments[i].parent_curve);
END_REPEAT;
END_IF;
END_IF;
RETURN(surfs);
END_FUNCTION;
(*
Argument definitions:
c: (input) a curve for which the basis_surface is to be determined.
EXPRESS specification:
*)
FUNCTION increasing_values_in_list (values : LIST[2:?] OF REAL) : BOOLEAN;
LOCAL result : BOOLEAN := TRUE; limit : INTEGER := SIZEOF(values); END_LOCAL; REPEAT i := 2 TO limit; IF values[i] <= values[i-1] THEN result := FALSE; END_IF; END_REPEAT; RETURN(result);
END_FUNCTION;
(*
Argument definitions:
values: (input) a list of real values to be tested.
EXPRESS specification:
*)
FUNCTION list_to_array (lis : LIST[0:?] OF GENERIC; low : INTEGER; u : INTEGER) : ARRAY[low:u] OF GENERIC;
LOCAL
n : INTEGER;
res : ARRAY [low:u] OF GENERIC : T;
END_LOCAL;
n := SIZEOF(lis);
IF (n <> (u-low +1)) THEN
RETURN(?);
ELSE
res := [lis[1] : n];
REPEAT i := 2 TO n;
res[low+i-1] := lis[i];
END_REPEAT;
RETURN(res);
END_IF;
END_FUNCTION;
(*
Argument definitions:
lis: (input) A list to be converted.
low: (input) An integer specifying the required lower index of the output array.
u: (input) An integer value for the upper index.
EXPRESS specification:
*)
FUNCTION make_array_of_array (lis : LIST[1:?] OF LIST[1:?] OF GENERIC; low1 : INTEGER; u1 : INTEGER; low2 : INTEGER; u2 : INTEGER) : ARRAY[low1:u1] OF ARRAY[low2:u2] OF GENERIC;
LOCAL
res : ARRAY[low1:u1] OF ARRAY [low2:u2] OF GENERIC : T;
END_LOCAL;
(* Check input dimensions for consistency *)
IF (u1-low1+1) <> SIZEOF(lis) THEN
RETURN (?);
END_IF;
IF (u2 - low2 + 1 ) <> SIZEOF(lis[1]) THEN
RETURN (?) ;
END_IF;
(* Initialise res with values from lis[1] *)
res := [list_to_array(lis[1], low2, u2) : (u1-low1 + 1)];
REPEAT i := 2 TO HIINDEX(lis);
IF (u2-low2+1) <> SIZEOF(lis[i]) THEN
RETURN (?);
END_IF;
res[low1+i-1] := list_to_array(lis[i], low2, u2);
END_REPEAT;
RETURN (res);
END_FUNCTION;
(*
Argument definitions:
lis: (input) A list of list to be converted.
low1: (input) An integer specifying the required lower index of the first output array.
u1: (input) An integer value for the upper index of the first output array.
low2: (input) An integer specifying the required lower index of the second output array.
u2: (input) An integer value for the upper index of the second output array.
EXPRESS specification:
*)
FUNCTION make_array_of_array_of_array (lis : LIST[1:?] OF LIST[1:?] OF LIST[1:?] OF GENERIC; low1 : INTEGER; u1 : INTEGER; low2 : INTEGER; u2 : INTEGER; low3 : INTEGER; u3 : INTEGER) : ARRAY[low1:u1] OF ARRAY[low2:u2] OF ARRAY[low3:u3] OF GENERIC;
LOCAL
res : ARRAY[low1:u1] OF ARRAY [low2:u2] OF
ARRAY[low3:u3] OF GENERIC : T;
END_LOCAL;
(* Check input dimensions for consistency *)
IF (u1-low1+1) <> SIZEOF(lis) THEN
RETURN (?);
END_IF;
IF (u2-low2+1) <> SIZEOF(lis[1]) THEN
RETURN (?);
END_IF;
(* Initialise res with values from lis[1] *)
res := [make_array_of_array(lis[1], low2, u2, low3, u3) : (u1-low1 + 1)];
REPEAT i := 2 TO HIINDEX(lis);
IF (u2-low2+1) <> SIZEOF(lis[i]) THEN
RETURN (?);
END_IF;
res[low1+i-1] := make_array_of_array(lis[i], low2, u2, low3, u3);
END_REPEAT;
RETURN (res);
END_FUNCTION;
(*
Argument definitions:
lis: (input) A list of list of list to be converted.
low1: (input) An integer specifying the required lower index of the first output array.
u1: (input) An integer value for the upper index of the first output array.
low2: (input) An integer specifying the required lower index of the second output array.
u2: (input) An integer value for the upper index of the second output array.
low3: (input) An integer specifying the required lower index of the third output array.
u3: (input) An integer value for the upper index of the third output array.
NOTE This function does not provide geometric founding for the direction returned, the caller of the the function is responsible for ensuring that it is used in a representation with a geometric_representation_context.
EXPRESS specification:
*)
FUNCTION normalise (arg : vector_or_direction) : vector_or_direction;
LOCAL
ndim : INTEGER;
v : direction := dummy_gri || direction ([1.0,0.0,0.0]);
result : vector_or_direction;
vec : vector := dummy_gri || vector (v, 1.0);
mag : REAL;
END_LOCAL;
IF NOT EXISTS (arg) THEN
result := ?;
(* When function is called with invalid data a NULL result is returned *)
ELSE
ndim := arg.dim;
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF(arg) THEN
BEGIN
v := dummy_gri || direction(arg\vector.orientation.direction_ratios);
IF arg\vector.magnitude = 0.0 THEN
RETURN(?);
ELSE
vec := dummy_gri || vector (v, 1.0);
END_IF;
END;
ELSE
v := dummy_gri || direction (arg.direction_ratios);
END_IF;
mag := 0.0;
REPEAT i := 1 TO ndim;
mag := mag + v.direction_ratios[i]*v.direction_ratios[i];
END_REPEAT;
IF mag > 0.0 THEN
mag := SQRT(mag);
REPEAT i := 1 TO ndim;
v.direction_ratios[i] := v.direction_ratios[i]/mag;
END_REPEAT;
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF(arg) THEN
vec.orientation := v;
result := vec;
ELSE
result := v;
END_IF;
ELSE
RETURN(?);
END_IF;
END_IF;
RETURN (result);
END_FUNCTION;
(*
Argument definitions:
arg: (input)a vector or direction to be normalised.
NOTE This function does not provide geometric founding for the direction returned, the caller of the the function is responsible for ensuring that it is used in a representation with a geometric_representation_context.
EXPRESS specification:
*)
FUNCTION orthogonal_complement (vec : direction) : direction;
LOCAL
result : direction ;
END_LOCAL;
IF (vec.dim <> 2) OR NOT EXISTS (vec) THEN
RETURN(?);
ELSE
result := dummy_gri || direction([-vec.direction_ratios[2],
vec.direction_ratios[1]]);
RETURN(result);
END_IF;
END_FUNCTION;
(*
Argument definitions:
vec: (input) A direction in 2D space.
EXPRESS specification:
*)
FUNCTION same_side (plane_pts : LIST[3:3] OF cartesian_point; test_points : LIST[2:?] OF cartesian_point) : BOOLEAN;
LOCAL
val1, val2 : REAL;
n : INTEGER;
END_LOCAL;
IF (plane_pts[1].dim = 2) OR (test_points[1].dim = 2) THEN
RETURN(?);
END_IF;
n := SIZEOF(test_points);
val1 := above_plane(plane_pts[1], plane_pts[2], plane_pts[3],
test_points[1] );
REPEAT i := 2 TO n;
val2 := above_plane(plane_pts[1], plane_pts[2], plane_pts[3],
test_points[i] );
IF (val1*val2 <= 0.0) THEN
RETURN(FALSE);
END_IF;
END_REPEAT;
RETURN(TRUE);
END_FUNCTION;
(*
Argument definitions:
plane_pts: (input) The LIST of 3 cartesian_points defining the plane used in the test.
test_points: (input) The LIST of cartesian_points to be tested for the property of lying on the same side of the plane.
NOTE This function does not provide geometric founding for the vector returned, the caller of the the function is responsible for ensuring that it is used in a representation with a geometric_representation_context.
EXPRESS specification:
*)
FUNCTION scalar_times_vector (scalar : REAL; vec : vector_or_direction) : vector;
LOCAL
v : direction;
mag : REAL;
result : vector;
END_LOCAL;
IF NOT EXISTS (scalar) OR NOT EXISTS (vec) THEN
RETURN (?) ;
ELSE
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF (vec) THEN
v := dummy_gri || direction(vec\vector.orientation.direction_ratios);
mag := scalar * vec\vector.magnitude;
ELSE
v := dummy_gri || direction(vec.direction_ratios);
mag := scalar;
END_IF;
IF (mag < 0.0 ) THEN
REPEAT i := 1 TO SIZEOF(v.direction_ratios);
v.direction_ratios[i] := -v.direction_ratios[i];
END_REPEAT;
mag := -mag;
END_IF;
result := dummy_gri || vector(normalise(v), mag);
END_IF;
RETURN (result);
END_FUNCTION;
(*
Argument definitions:
scalar: (input) a real number to participate in the product.
vec: (input) a vector or direction which is to be multiplied.
NOTE This function does not provide geometric founding for the direction returned, the caller of the the function is responsible for ensuring that it is used in a representation with a geometric_representation_context.
EXPRESS specification:
*)
FUNCTION second_proj_axis (z_axis : direction; x_axis : direction; arg : direction) : direction;
LOCAL
y_axis : vector;
v : direction;
temp : vector;
END_LOCAL;
IF NOT EXISTS(arg) THEN
v := dummy_gri || direction([0.0,1.0,0.0]);
ELSE
v := arg;
END_IF;
temp := scalar_times_vector(dot_product(v, z_axis), z_axis);
y_axis := vector_difference(v, temp);
temp := scalar_times_vector(dot_product(v, x_axis), x_axis);
y_axis := vector_difference(y_axis, temp);
y_axis := normalise(y_axis);
RETURN(y_axis.orientation);
END_FUNCTION;
(*
Argument definitions:
z_axis: (input) a defining a local Z axis.
x_axis: (input) a direction not parallel to z_axis.
arg: (input) a direction which is used as the first approximation to the direction of y_axis.
EXPRESS specification:
*)
FUNCTION surface_weights_positive (b : rational_b_spline_surface) : BOOLEAN;
LOCAL
result : BOOLEAN := TRUE;
END_LOCAL;
REPEAT i := 0 TO b.u_upper;
REPEAT j := 0 TO b.v_upper;
IF (b.weights[i][j] <= 0.0) THEN
result := FALSE;
RETURN(result);
END_IF;
END_REPEAT;
END_REPEAT;
RETURN(result);
END_FUNCTION;
(*
Argument definitions:
b: (input) a rational_b_spline_surface for which the weight values are to be tested.
NOTE This function does not provide geometric founding for the vector returned, the caller of the the function is responsible for ensuring that it is used in a representation with a geometric_representation_context
EXPRESS specification:
*)
FUNCTION vector_difference (arg1 : vector_or_direction; arg2 : vector_or_direction) : vector;
LOCAL
result : vector;
res, vec1, vec2 : direction;
mag, mag1, mag2 : REAL;
ndim : INTEGER;
END_LOCAL;
IF ((NOT EXISTS (arg1)) OR (NOT EXISTS (arg2))) OR (arg1.dim <> arg2.dim)
THEN
RETURN (?) ;
ELSE
BEGIN
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF(arg1) THEN
mag1 := arg1\vector.magnitude;
vec1 := arg1\vector.orientation;
ELSE
mag1 := 1.0;
vec1 := arg1;
END_IF;
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF(arg2) THEN
mag2 := arg2\vector.magnitude;
vec2 := arg2\vector.orientation;
ELSE
mag2 := 1.0;
vec2 := arg2;
END_IF;
vec1 := normalise (vec1);
vec2 := normalise (vec2);
ndim := SIZEOF(vec1.direction_ratios);
mag := 0.0;
res := dummy_gri || direction(vec1.direction_ratios);
REPEAT i := 1 TO ndim;
res.direction_ratios[i] := mag1*vec1.direction_ratios[i] -
mag2*vec2.direction_ratios[i];
mag := mag + (res.direction_ratios[i]*res.direction_ratios[i]);
END_REPEAT;
IF (mag > 0.0 ) THEN
result := dummy_gri || vector( res, SQRT(mag));
ELSE
result := dummy_gri || vector( vec1, 0.0);
END_IF;
END;
END_IF;
RETURN (result);
END_FUNCTION;
(*
Argument definitions:
arg1: (input) a directions or vector defining first operand in the vector difference operation;
arg2: (input) a directions or vector defining the second operand for vector difference;
NOTE This function does not provide geometric founding for the vector returned, the caller of the the function is responsible for ensuring that it is used in a representation with a geometric_representation_context
EXPRESS specification:
*)
FUNCTION vector_sum (arg1 : vector_or_direction; arg2 : vector_or_direction) : vector;
LOCAL
result : vector;
res, vec1, vec2 : direction;
mag, mag1, mag2 : REAL;
ndim : INTEGER;
END_LOCAL;
IF ((NOT EXISTS (arg1)) OR (NOT EXISTS (arg2))) OR (arg1.dim <> arg2.dim)
THEN
RETURN (?) ;
ELSE
BEGIN
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF(arg1) THEN
mag1 := arg1\vector.magnitude;
vec1 := arg1\vector.orientation;
ELSE
mag1 := 1.0;
vec1 := arg1;
END_IF;
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF(arg2) THEN
mag2 := arg2\vector.magnitude;
vec2 := arg2\vector.orientation;
ELSE
mag2 := 1.0;
vec2 := arg2;
END_IF;
vec1 := normalise (vec1);
vec2 := normalise (vec2);
ndim := SIZEOF(vec1.direction_ratios);
mag := 0.0;
res := dummy_gri || direction(vec1.direction_ratios);
REPEAT i := 1 TO ndim;
res.direction_ratios[i] := mag1*vec1.direction_ratios[i] +
mag2*vec2.direction_ratios[i];
mag := mag + (res.direction_ratios[i]*res.direction_ratios[i]);
END_REPEAT;
IF (mag > 0.0 ) THEN
result := dummy_gri || vector( res, SQRT(mag));
ELSE
result := dummy_gri || vector( vec1, 0.0);
END_IF;
END;
END_IF;
RETURN (result);
END_FUNCTION;
(*
Argument definitions:
arg1: (input) a vector or direction defining the first operand in vector sum operation..
arg2: (input) a vector or direction defining the second operand for vector sum operation.
EXPRESS specification:
*)
FUNCTION volume_weights_positive (b : rational_b_spline_volume) : BOOLEAN;
LOCAL
result : BOOLEAN := TRUE;
END_LOCAL;
REPEAT i := 0 TO b.u_upper;
REPEAT j := 0 TO b.v_upper;
REPEAT k := 0 TO b.w_upper;
IF (b.weights[i][j][k] <= 0.0) THEN
result := FALSE;
RETURN(result);
END_IF;
END_REPEAT;
END_REPEAT;
END_REPEAT;
RETURN(result);
END_FUNCTION;
(*
Argument definitions:
b: (input) a rational_b_spline_volume for which the weight values are to be tested.
EXPRESS specification:
*)
FUNCTION weights_positive (weights : LIST[0:?] OF REAL) : BOOLEAN;
LOCAL result : BOOLEAN := TRUE; END_LOCAL; REPEAT i := 1 TO SIZEOF(weights); IF weights[i] <= 0.0 THEN result := FALSE; RETURN(result); END_IF; END_REPEAT; RETURN(result);
END_FUNCTION;
(*
Argument definitions:
weights: (input) a LIST of weight values to be tested. are to be tested.
All geometric_representation_items are geometrically founded in one or more geometric_representation_context coordinate spaces.
The rule compatible_dimension ensures that when geometric_representation_items are geometrically founded together in a coordinate space, they have the same coordinate space dimension_count by ensuring that each matches the dimension_count of the coordinate space in which it is geometrically founded. The rule returns TRUE when there are no cartesian_point, no direction, and no geometric_representation_context.
NOTE 1 Two-dimensional geometric_representation_items that are geometrically founded in a geometric_representation_context are only geometrically founded in context with a coordinate_space_dimension of 2. All geometric_representation_items founded in such a context are two-dimensional. All other values of dimension_count behave similarly.
EXPRESS specification:
*)
RULE compatible_dimension FOR
(cartesian_point,direction,geometric_representation_context);WHERE
WR1: ((SIZEOF(cartesian_point) = 0) AND (SIZEOF(direction) = 0) AND (SIZEOF(geometric_representation_context) = 0)) OR
check_geometric_dimension(cartesian_point, direction, geometric_representation_context);
END_RULE;
(*
Argument definitions:
cartesian_point : the set of all instances of cartesian_point.
direction : the set of all instances of direction.
geometric_representation_context : the set of all instances of geometric_representation_context.
Formal propositions:
WR1: There shall be no cartesian_point that has a number of coordinates that differs from the coordinate_space_dimension of the geometric_representation_contexts in which it is geometrically founded; there shall be no direction that has a number of direction_ratios that differs from the coordinate_space_dimension of the geometric_representation_contexts in which it is geometrically founded. These properties are verifieded by the function check_geometric_dimension.
NOTE 2 A check of only cartesian_points and directions is sufficient for all geometric_representation_items because:
All geometric_representation_items appear in trees of representation_items descending from the items attribute of entity representation. See WR1 of entity representation_item in ISO 10303-43.
Each geometric_representation_item gains its position and orientation information only by being, or referring to, a cartesian_point or direction entity in such a tree. In many cases this reference is made via an placement.
No other use of any geometric_representation_item is allowed that would associate it with a coordinate space or otherwise assign a dimension_count.
*)
END_SCHEMA; -- geometry_schema
(*
© ISO 2021 — All rights reserved