Application module: Basic geometry ISO/TS 10303-1652:2019(E)
© ISO

Cover page
Table of contents
Copyright
Foreword
Introduction
1 Scope
2 Normative references
3 Terms, definitions and abbreviated terms
    3.1 Terms and definitions
    3.2 Abbreviated terms

4 Information requirements
   4.1 Required AM ARMs
   4.2 ARM entity definitions
   4.3 ARM subtype constraint definitions
5 Module interpreted model
   5.1 Mapping specification
   5.2 MIM EXPRESS short listing

A MIM short names
B Information object registration
C ARM EXPRESS-G   EXPRESS-G
D MIM EXPRESS-G   EXPRESS-G
E Computer interpretable listings
F Change history
Bibliography
Index

4 Information requirements

This clause specifies the information requirements for the Basic geometry application module. The information requirements are specified as the Application Reference Model (ARM) of this application module.

NOTE 1  A graphical representation of the information requirements is given in Annex C.

NOTE 2  The mapping specification is specified in 5.1. It shows how the information requirements are met by using common resources and constructs defined or imported in the MIM schema of this application module.

This clause defines the information requirements to which implementations shall conform using the EXPRESS language as defined in ISO 10303-11. The following begins the Basic_geometry_arm schema and identifies the necessary external references.

EXPRESS specification:

*)
SCHEMA Basic_geometry_arm;
(*

4.1 Required AM ARMs

The following EXPRESS interface statements specify the elements imported from the ARMs of other application modules.

EXPRESS specification:

*)
USE FROM Elemental_geometric_shape_arm;    --  ISO/TS 10303-1004

USE FROM Parametric_representation_arm;    --  ISO/TS 10303-1813
(*

NOTE 1   The schemas referenced above are specified in the following part of ISO 10303:

Elemental_geometric_shape_arm ISO/TS 10303-1004
Parametric_representation_arm ISO/TS 10303-1813

NOTE 2   See Annex C, Figures C.1and C.2 for a graphical representation of this schema.

4.2 ARM entity definitions

This subclause specifies the ARM entities for this module. Each ARM application entity is an atomic element that embodies a unique application concept and contains attributes specifying the data elements of the entity. The ARM entities and definitions are specified below.

4.2.1 Bounded_curve   EXPRESS-GMapping table

A Bounded_curve is a type of Curve which has finite arc length and identifiable start and end points.

NOTE    A closed curve such as a circle or ellipse is not a bounded curve.

EXPRESS specification:

*)
ENTITY Bounded_curve
  ABSTRACT SUPERTYPE
  SUBTYPE OF (Curve);
END_ENTITY;
(*

4.2.2 Bounded_surface   EXPRESS-GMapping table

A Bounded_surface is a type of Surface which has finite area and identifiable boundaries.

NOTE    A surface, such as a cylinder or sphere, closed in one, or two, parametric directions is not a bounded surface.

EXPRESS specification:

*)
ENTITY Bounded_surface
  ABSTRACT SUPERTYPE
  SUBTYPE OF (Surface);
END_ENTITY;
(*

4.2.3 Circle   EXPRESS-GMapping table

A Circle is a type of Conic in which all points are equidistant from the centre. A circle can be a 2D curve or a planar curve in 3D space.

NOTE    The parameterization of the circle is defined in the corresponding MIM entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Circle
  SUBTYPE OF (Conic);
  radius : positive_length_measure;
END_ENTITY;
(*

Attribute definitions:

radius: the distance from the centre to all points of the curve.

4.2.4 Conic   EXPRESS-GMapping table

A Conic is a type of Curve that is the intersection of a cone and a plane. A conic can be a 2D curve or a planar curve in 3D space.

EXPRESS specification:

*)
ENTITY Conic
  SUPERTYPE OF (ONEOF (Circle,
                       Ellipse,
                       Hyperbola,
                       Parabola))
  SUBTYPE OF (Curve);
  position : Axis_placement;
END_ENTITY;
(*

Attribute definitions:

position: an Axis_placement that defines the location and orientation of the conic. The plane of the conic is defined by ref_direction, axis and the location which is a reference point in the plane.

4.2.5 Conical_surface   EXPRESS-GMapping table

A Conical_surface is a type of Surface that has the shape of a cone. A Conical_surface is produced by revolving a line about an intersecting central axis.

NOTE    The parameterization of the Conical_surface is defined in the corresponding MIM entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Conical_surface
  SUBTYPE OF (Surface);
  position : Axis_placement_3d;
  radius : positive_length_measure;
  semi_angle : plane_angle_measure;
END_ENTITY;
(*

Attribute definitions:

position: an Axis_placement_3d that defines the location and orientation of the surface. The axis of the Conical_surface passes through the location and is normal to the plane of ref_direction and axis.

radius: the radius of the circular curve of intersection between the cone and a plane perpendicular to the axis of the cone passing through the location. This will have value 0.0 if the location is at the apex of the cone.

semi_angle: the cone semi-angle, this is the angle between the axis of the Conical_surface and the generating line.

4.2.6 Curve   EXPRESS-GMapping table

A Curve is a type of Detailed_geometric_model_element. A Curve is the path of a point moving through its three-dimensional coordinate space or of a point moving through its two-dimensional coordinate space. A Curve shall be arc-wise connected. A Curve shall have an arc length greater than zero.

NOTE    The exact form of the curve is defined by its subtypes, each curve has a unique parameterization r = λ(u), this parameterization is defined with the corresponding ARM object and is used in the definition of Point_on_curve .

EXPRESS specification:

*)
ENTITY Curve
  SUPERTYPE OF (ONEOF (Conic,
                       Line))
  SUBTYPE OF (Detailed_geometric_model_element);
END_ENTITY;
(*

4.2.7 Cylindrical_point   EXPRESS-GMapping table

A Cylindrical_point is a type of Cartesian_point which uses a three dimensional cylindrical polar coordinate system, centred at the origin of the corresponding Cartesian coordinate system, to define its location.

EXPRESS specification:

*)
ENTITY Cylindrical_point
  SUBTYPE OF (Cartesian_point);
  r : positive_length_measure;
  theta : plane_angle_measure;
  z : length_measure;
DERIVE
  SELF\Cartesian_point.coordinates : LIST[3:3] OF length_measure := [r*cos(theta), r*sin(theta), z];
END_ENTITY;
(*

Attribute definitions:

r: the distance from the point to the z axis;

theta: the angle between the plane containing the point and the z axis and the xz plane;

z: the distance from the xy plane to the point.

coordinates: the rectangular Cartesian coordinates of this point;

4.2.8 Cylindrical_surface   EXPRESS-GMapping table

A Cylindrical_surface is a type of Surface that has the shape of a circular cylinder.

NOTE    The parameterization of the Cylindrical_surface is defined in the corresponding MIM entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Cylindrical_surface
  SUBTYPE OF (Surface);
  position : Axis_placement_3d;
  radius : positive_length_measure;
END_ENTITY;
(*

Attribute definitions:

position: an Axis_placement_3d that defines the location and orientation of the surface. The axis of the Cylindrical_surface passes through the location and is normal to the plane of ref_direction and axis.

radius: the radius of the circular curve of intersection between the surface of the cylinder and a plane perpendicular to the axis of the Cylindrical_surface.

4.2.9 Degenerate_pcurve   EXPRESS-GMapping table

A Degenerate_pcurve is a type of Point that is defined as a parameter space curve, but in three-dimensional model space it collapses to a single point. It is thus a subtype of Point, not of Curve.

NOTE    For example, the apex of a cone could be represented as a degenerate_pcurve.

EXPRESS specification:

*)
ENTITY Degenerate_pcurve
  SUBTYPE OF (Point);
  basis_surface : Surface;
  reference_to_curve : Definitional_representation;
WHERE
  WR1: SIZEOF(reference_to_curve\Representation.items) = 1;
  WR2: 'BASIC_GEOMETRY_ARM.CURVE' IN TYPEOF (reference_to_curve\Representation.items[1]);
END_ENTITY;
(*

Attribute definitions:

basis_surface: the surface on which the Degenerate_pcurve lies;

reference_to_curve: the association of the Degenerate_pcurve and the parameter space curve which degenerates to the (equivalent) point.

Formal propositions:

WR1: The set of items in the Definitional_representation entity corresponding to the reference_to_curve shall have exactly one element ;

WR2: The unique item in the set shall be a Curve.

Informal propositions:

IP1: Regarded as a curve in model space, the Degenerate_pcurve shall have zero arc length;

IP2: The dimensionality of this parameter space curve shall be 2.

4.2.10 Ellipse   EXPRESS-GMapping table

An Ellipse is a type of Conic which is a closed curve defined by the lengths of its two diameters. An ellipse can be a 2D curve or a planar curve in 3D space.

NOTE    The parameterization of the Ellipse is defined in the corresponding MIM entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Ellipse
  SUBTYPE OF (Conic);
  first_semi_axis : positive_length_measure;
  second_semi_axis : positive_length_measure;
END_ENTITY;
(*

Attribute definitions:

first_semi_axis: half the length of the first diameter of the Ellipse.

second_semi_axis: half the length of the second diameter of the Ellipse.

4.2.11 Extruded_surface   EXPRESS-GMapping table

An Extruded_surface is a type of Swept_surface that is the result of sweeping the swept_curve in the direction of the extrusion_axis. The resulting surface is a ruled surface with rulings parallel to the extrusion_axis.

NOTE    The parameterization of the Extruded_surface is defined in the corresponding MIM entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Extruded_surface
  SUBTYPE OF (Swept_surface);
  extrusion_axis : Direction;
END_ENTITY;
(*

Attribute definitions:

extrusion_axis: a Direction that defines the sweeping direction for the surface.

4.2.12 Hyperbola   EXPRESS-GMapping table

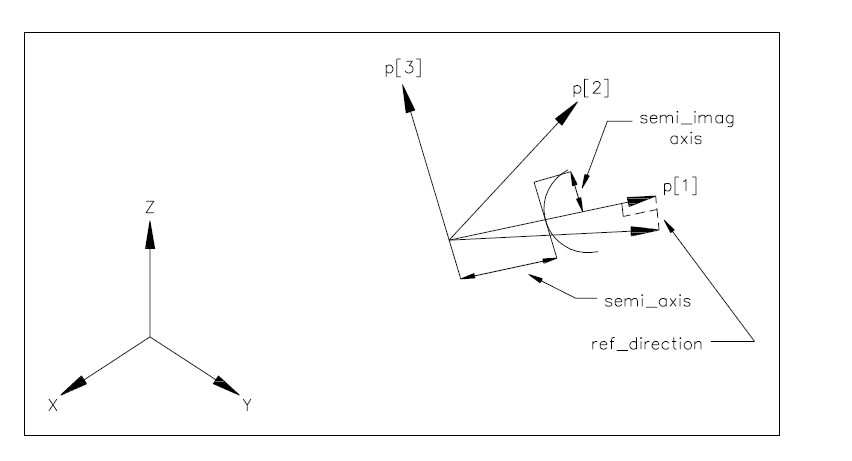
An Hyperbola is a type of Conic which is a curve with two branches produced by intersecting a double cone with a plane at an acute angle to its central axis. A hyperbola can be a 2D curve or a planar curve in 3D space.

NOTE 1   The parameterization of the Hyperbola is defined in the corresponding MIM entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Hyperbola
  SUBTYPE OF (Conic);
  semi_axis : positive_length_measure;
  imaginary_semi_axis : positive_length_measure;
END_ENTITY;
(*

Attribute definitions:

semi_axis: half the minimum distance between the two branches of the Hyperbola.

imaginary_semi_axis: the length of semi imaginary axis of the Hyperbola.

NOTE 2   The semi imaginary axis is sometimes called the minor or conjugate axis of the hyperbola, and the semi_axis is also sometimes called the major axis.

NOTE 3   The asymptotes to the hyperbola pass through the central point and have a slope relative to the central axis of R2: R1, where R2 = semi_imag_axis and R1 = semi_axis.

NOTE 4   See Figure 1 for interpretation of attributes.



Figure 1 —  Hyperbola

Figure 1 —  Hyperbola

4.2.13 Line   EXPRESS-GMapping table

A Line is a type of Curve that is straight. A Line is considered infinite.

NOTE    The parameterization of the Line is defined in the corresponding MIM entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Line
  SUBTYPE OF (Curve);
  point : Cartesian_point;
  line_direction : Direction;
END_ENTITY;
(*

Attribute definitions:

point: a point through which the line passes.

line_direction: the direction of the line.

4.2.14 Parabola   EXPRESS-GMapping table

A Parabola is a type of Conic which is an unbounded curve produced by intersecting a cone with a plane parallel to a generating line at an angle to its central axis equal to the semi-angle. A Parabola can be a 2D curve or a planar curve in 3D space.

NOTE    The parameterization of the Parabola is defined in the corresponding MIM entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Parabola
  SUBTYPE OF (Conic);
  focal_distance : length_measure;
WHERE
  WR1: focal_distance <> 0.0;
END_ENTITY;
(*

Attribute definitions:

focal_distance: the distance between the focal point of the Parabola and the apex of the cone.

Formal propositions:

WR1: The focal_distance shall be non-zero.

4.2.15 Plane   EXPRESS-GMapping table

A Plane is a type of Surface that is flat. A Plane is considered infinite.

NOTE    The parameterization of the Plane is defined in the corresponding MIM entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Plane
  SUBTYPE OF (Surface);
  position : Axis_placement_3d;
END_ENTITY;
(*

Attribute definitions:

position: an Axis_placement_3d that defines the location and orientation of the plane.

4.2.16 Point_on_curve   EXPRESS-GMapping table

A Point_on_curve is a type of Detailed_geometric_model_element that characterizes a point which lies on a curve. It results from the evaluation of the function that defines the Curve with a particular parameter.

EXPRESS specification:

*)
ENTITY Point_on_curve
  SUBTYPE OF (Point);
  supporting_curve : Curve;
END_ENTITY;
(*

Attribute definitions:

supporting_curve: specifies the Curve containing the Point_on_curve.

4.2.17 Point_on_surface   EXPRESS-GMapping table

A Point_on_surface is a type of Detailed_geometric_model_element that characterizes a point that lies on a surface. It either results from the evaluation of the function that defines the Surface parameterization with a particular pair of parameter values or from the evaluation of a point where a curve on the surface collapses.

EXPRESS specification:

*)
ENTITY Point_on_surface
  SUBTYPE OF (Point);
  supporting_surface : Surface;
END_ENTITY;
(*

Attribute definitions:

supporting_surface: specifies the Surface containing the Point_on_surface.

4.2.18 Polar_point   EXPRESS-GMapping table

A Polar_point is a type of Cartesian_point which uses a two dimensional polar coordinate system, centred at the origin of the corresponding Cartesian coordinate system, to define its location.

EXPRESS specification:

*)
ENTITY Polar_point
  SUBTYPE OF (Cartesian_point);
  r : positive_length_measure;
  theta : plane_angle_measure;
DERIVE
  SELF\Cartesian_point.coordinates : LIST[2:2] OF length_measure := [r*cos(theta), r*sin(theta)];
END_ENTITY;
(*

Attribute definitions:

r: the distance from the point to the origin;

theta: the angle between the x axis and the line joining the origin to the point.

coordinates: the rectangular cartesian coordinates of this point;

4.2.19 Spherical_point   EXPRESS-GMapping table

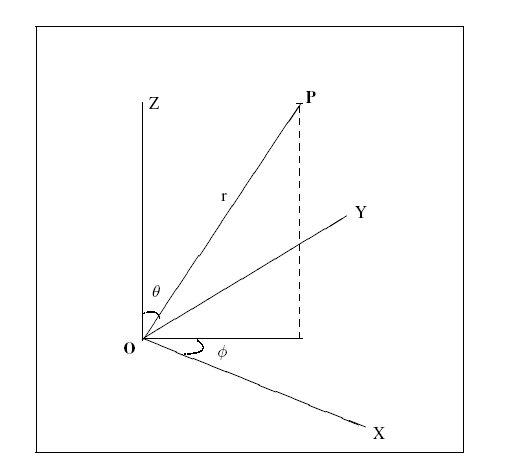
A Spherical_point is a type of Cartesian_point which uses a three dimensional spherical polar coordinate system, centred at the origin of the corresponding Cartesian coordinate system, to define its location.

EXPRESS specification:

*)
ENTITY Spherical_point
  SUBTYPE OF (Cartesian_point);
  r : positive_length_measure;
  theta : plane_angle_measure;
  phi : plane_angle_measure;
DERIVE
  SELF\Cartesian_point.coordinates : LIST[3:3] OF length_measure := [r*sin(theta)*cos(phi), r*sin(theta)*sin(phi), r*cos(theta)];
END_ENTITY;
(*

Attribute definitions:

r: the distance from the point to the z axis;

theta: the angle θ between the z axis and the line joining the origin to the point;

phi: the angle φ measured from the x axis to the projection onto the xy plane of the line from the origin to the point.

coordinates: the rectangular cartesian coordinates of this point;

NOTE    See Figure 2 for an illustration of the attributes.



Figure 2 —  Spherical point attributes

Figure 2 —  Spherical point attributes

4.2.20 Spherical_surface   EXPRESS-GMapping table

A Spherical_surface is a type of Surface that has the shape of a sphere.

NOTE    The parameterization of the Spherical_surface is defined in the corresponding MIM entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Spherical_surface
  SUBTYPE OF (Surface);
  position : Axis_placement_3d;
  radius : positive_length_measure;
END_ENTITY;
(*

Attribute definitions:

position: an Axis_placement_3d that defines the location and orientation of the surface for the purposes of parameterization. The centre of the Spherical_surface is at the location

radius: the radius of the Spherical_surface.

4.2.21 Surface   EXPRESS-GMapping table

A Surface is a type of Detailed_geometric_model_element that is a continuous 2D subspace of a 3D space.

NOTE 1   A Surface may, exceptionally, not be manifold.

NOTE 2   The Surface entity is a supertype of various specific kinds of surfaces. The definition of some of these specific types is outside the scope of the present module.

NOTE 3   Each surface has a unique parameterization S = λ(u,v), this parameterization is defined with the corresponding ARM object and is used in the definition of Point_on_surface .

EXPRESS specification:

*)
ENTITY Surface
  SUPERTYPE OF (ONEOF (Conical_surface,
                       Cylindrical_surface,
                       Plane,
                       Spherical_surface,
                       Swept_surface,
                       Toroidal_surface))
  SUBTYPE OF (Detailed_geometric_model_element);
END_ENTITY;
(*

4.2.22 Surface_of_revolution   EXPRESS-GMapping table

A Surface_of_revolution is a type of Swept_surface that is the result of revolving the swept_curve about an axis.

NOTE    The parameterization of the Surface_of_revolution is defined in the corresponding entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Surface_of_revolution
  SUBTYPE OF (Swept_surface);
  axis_direction : Direction;
  axis_point : Cartesian_point;
END_ENTITY;
(*

Attribute definitions:

axis_direction: a Direction that defines the direction of the axis of revolution.

axis_point: a Cartesian_point that lies on the axis of revolution.

4.2.23 Swept_surface   EXPRESS-GMapping table

A Swept_surface is a type of Surface that is the result of sweeping a Curve. The direction of sweeping is defined with the subtypes of this entity.

EXPRESS specification:

*)
ENTITY Swept_surface
  SUPERTYPE OF (ONEOF (Extruded_surface,
                       Surface_of_revolution))
  SUBTYPE OF (Surface);
  swept_curve : Curve;
END_ENTITY;
(*

Attribute definitions:

swept_curve: the Curve that is swept to generate the Swept_surface.

4.2.24 Toroidal_surface   EXPRESS-GMapping table

A Toroidal_surface is a type of Surface that has the shape of a torus. The surface can be generated by revolving a circle of radius minor_radius about an axis in the plane of the circle.

NOTE    The parameterization of the Toroidal_surface is defined in the corresponding MIM entity from ISO 10303-42.

EXPRESS specification:

*)
ENTITY Toroidal_surface
  SUBTYPE OF (Surface);
  position : Axis_placement_3d;
  radius : positive_length_measure;
  minor_radius : positive_length_measure;
END_ENTITY;
(*

Attribute definitions:

position: an Axis_placement_3d that defines the location and orientation of the surface. The centre of the Toroidal_surface is at the location. The plane of the ref_direction and the axis is a central plane of symmetry of the Toroidal_surface. The normal to this plane is the central axis of the surface.

radius: the distance from the central axis of the Toroidal_surface to the centre of one of the circles produced by intersecting the Toroidal_surface with a plane containing the central axis. The surface can be produced by sweeping a circle of radius minor_radius along a circle of radius radius.

minor_radius: the radius of one of the circles produced by intersecting the Toroidal_surface with a plane containing the central axis.

4.3 ARM subtype constraint definitions

This subclause specifies the ARM subtype constraints for this module. Each subtype constraint places constraints on the possible super-type / subtype instantiations. The ARM subtype constraints and definitions are specified below.

4.3.1 alternate_geometry_items   EXPRESS-GMapping table

The alternate_geometry_items constraint specifies a constraint that applies to instances of Detailed_geometric_model_element and enforces the rule that its subtypes Direction, Axis_placement, Cartesian_transformation_2d, Cartesian_transformation_3d, Curve and Surface are exclusive.

EXPRESS specification:

*)
SUBTYPE_CONSTRAINT alternate_geometry_items FOR Detailed_geometric_model_element;
  ONEOF (Direction,
         Axis_placement,
         Cartesian_transformation_2d,
         Cartesian_transformation_3d,
         Curve,
         Surface);
END_SUBTYPE_CONSTRAINT;
(*

4.3.2 point_subtypes   EXPRESS-GMapping table

The point_subtypes constraint specifies a constraint that applies to instances of Point and enforces the rule that its subtypes Cartesian_point, Degenerate_pcurve, Point_on_curve and Point_on_surface are exclusive.

EXPRESS specification:

*)
SUBTYPE_CONSTRAINT point_subtypes FOR Point;
  ONEOF (Cartesian_point,
         Degenerate_pcurve,
         Point_on_curve,
         Point_on_surface);
END_SUBTYPE_CONSTRAINT;
(*

4.3.3 cartesian_point_subtypes   EXPRESS-GMapping table

The cartesian_point_subtypes constraint specifies a constraint that applies to instances of Cartesian_point and enforces the rule that its subtypes Cylindrical_point, Polar_point and Spherical_point are exclusive.

EXPRESS specification:

*)
SUBTYPE_CONSTRAINT cartesian_point_subtypes FOR Cartesian_point;
  ONEOF (Cylindrical_point,
         Polar_point,
         Spherical_point);
END_SUBTYPE_CONSTRAINT;
(*



*)
END_SCHEMA;  -- Basic_geometry_arm
(*

© ISO 2019 — All rights reserved